Flutter for OpenHarmony 实战：七巧板游戏几何图形与多边形碰撞

欢迎加入开源鸿蒙跨平台社区：开源鸿蒙跨平台开发者社区

前言

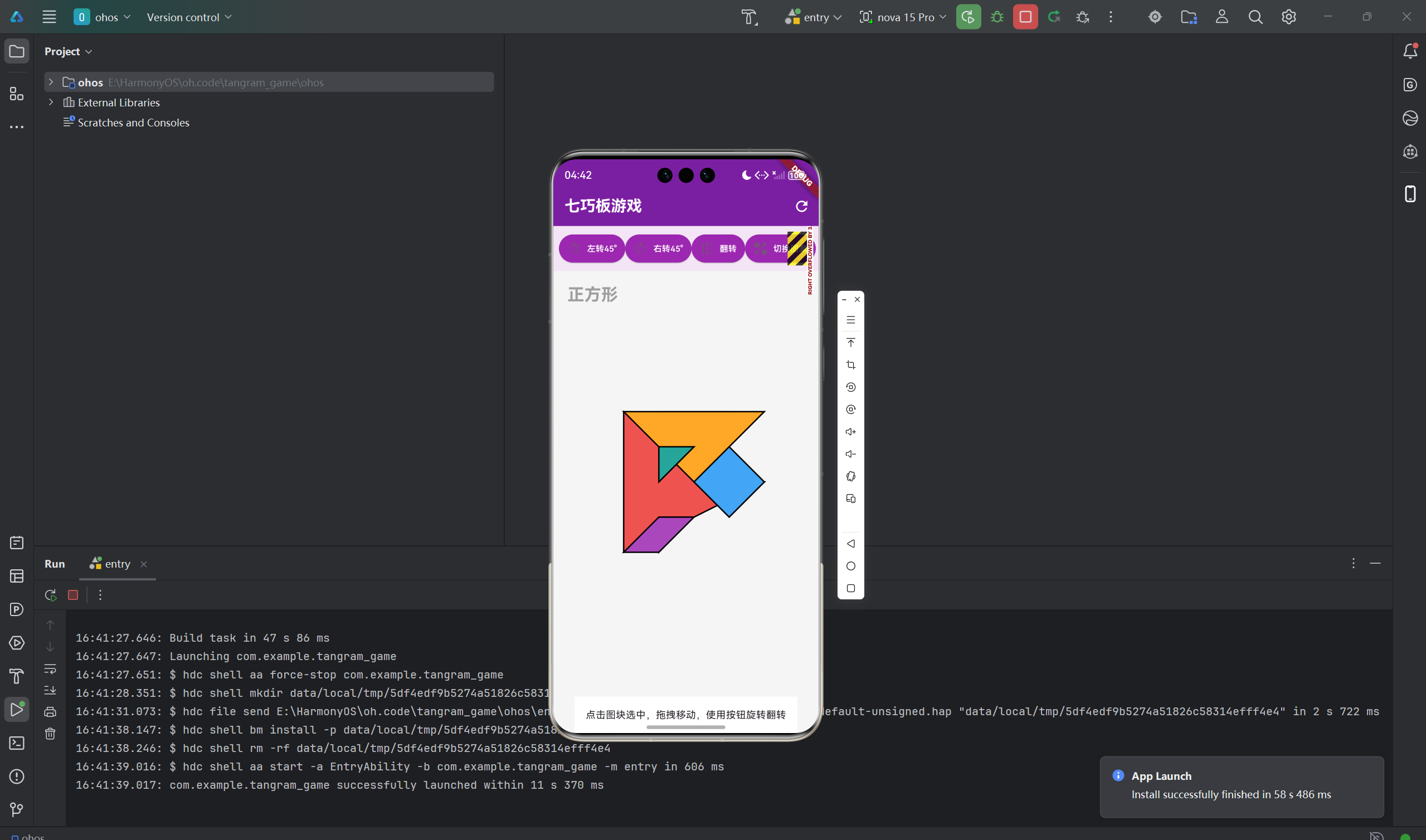
在这里插入图片描述

七巧板游戏的核心技术挑战在于如何精确表示各种几何图形，以及如何实现复杂的多边形碰撞检测。本文将深入分析七巧板的数据结构设计、射线法碰撞检测算法、线段相交判断、图块选择系统以及旋转和翻转的数学原理。

一、七巧板数据结构

1.1 图块类定义

class TangramPiece {
  final int id;
  final String name;
  List<Offset> vertices;
  final Color color;

  TangramPiece({
    required this.id,
    required this.name,
    required this.vertices,
    required this.color,
  });
}

每个图块包含唯一标识、名称、顶点列表和颜色。vertices使用List存储多边形的各个顶点，这种设计可以表示任意多边形。

1.2 标准七巧板组成

List<TangramPiece> _createPieces() {
  const double unitSize = 50;
  const double centerX = 200;
  const double centerY = 300;

  return [
    TangramPiece(
      id: 1,
      name: '大三角形1',
      vertices: [
        Offset(centerX - 2 * unitSize, centerY - 2 * unitSize),
        Offset(centerX + 2 * unitSize, centerY),
        Offset(centerX - 2 * unitSize, centerY + 2 * unitSize),
      ],
      color: Colors.red.shade400,
    ),
    // ... 其他6块
  ];
}

七巧板由7块组成：2个大三角形、1个中三角形、2个小三角形、1个正方形、1个平行四边形。使用相对坐标系统，以屏幕中心为基准点，unitSize为基本单位长度。

1.3 顶点坐标系统

const double centerX = 200;
const double centerY = 300;
const double unitSize = 50;

所有图块的顶点都相对于这个中心点定义，unitSize为基本长度单位。这种相对坐标系统使得调整整体位置变得简单，只需修改centerX和centerY。

二、射线法碰撞检测

2.1 点在多边形内判断

bool _isPointInPolygon(Offset point, List<Offset> vertices) {
  int intersectCount = 0;

  for (int i = 0; i < vertices.length; i++) {
    Offset v1 = vertices[i];
    Offset v2 = vertices[(i + 1) % vertices.length];

    if (_isIntersect(point, Offset(point.dx + 500, point.dy), v1, v2)) {
      intersectCount++;
    }
  }

  return intersectCount % 2 == 1;
}

射线法的基本原理：从测试点向右引一条水平射线，计算这条射线与多边形边界的交点数量。如果交点数量为奇数，则点在多边形内部；如果为偶数，则在外部。

2.2 射线方向选择

Offset(point.dx + 500, point.dy)

射线向右延伸500像素，这个长度足够覆盖大多数情况。选择水平射线简化了计算，因为只需要考虑Y坐标相等的情况。

2.3 模运算处理边界

Offset v2 = vertices[(i + 1) % vertices.length];

使用模运算确保最后一个顶点与第一个顶点相连，形成闭合多边形。这是处理循环数组的常用技巧。

三、线段相交判断

3.1 快速排斥实验

bool _isIntersect(Offset p1, Offset p2, Offset p3, Offset p4) {
  if (max(p1.dx, p2.dx) < min(p3.dx, p4.dx)) return false;
  if (max(p3.dx, p4.dx) < min(p1.dx, p2.dx)) return false;
  if (max(p1.dy, p2.dy) < min(p3.dy, p4.dy)) return false;
  if (max(p3.dy, p4.dy) < min(p1.dy, p2.dy)) return false;

  // 跨立实验
}

首先检查两个线段的包围盒是否重叠。如果任一线段的最大值小于另一线段的最小值，则不可能相交。这种快速排斥实验可以排除大多数不相交的情况。

3.2 跨立实验

final cross1 = _crossProduct(p3, p4, p1);
final cross2 = _crossProduct(p3, p4, p2);
final cross3 = _crossProduct(p1, p2, p3);
final cross4 = _crossProduct(p1, p2, p4);

return cross1 * cross2 <= 0 && cross3 * cross4 <= 0;

跨立实验检查两条线段是否相互跨越。如果一条线段的两个端点分别在另一条线段的两侧，则两线段相交。使用叉积判断点与直线的位置关系。

3.3 叉积计算

double _crossProduct(Offset p1, Offset p2, Offset p3) {
  return (p2.dx - p1.dx) * (p3.dy - p1.dy) -
         (p2.dy - p1.dy) * (p3.dx - p1.dx);
}

叉积的几何意义：判断点P3在直线P1P2的哪一侧。正值表示在左侧，负值表示在右侧，零表示在直线上。

四、图块选择系统

4.1 点击检测流程

void _handlePanStart(DragStartDetails details) {
  final localPosition = details.localPosition;

  for (int i = pieces.length - 1; i >= 0; i--) {
    if (_isPointInPiece(localPosition, pieces[i])) {
      setState(() {
        selectedPiece = pieces[i];
        dragStartPosition = localPosition;
        pieces.removeAt(i);
        pieces.add(selectedPiece!);
      });
      break;
    }
  }
}

从上层到底层遍历图块，找到第一个包含点击点的图块。选中后将图块移到数组末尾（最上层），确保选中的图块显示在最前面。

4.2 选择状态管理

TangramPiece? selectedPiece;
Offset? dragStartPosition;

使用可空类型记录当前选中的图块和拖拽起始位置。可空类型允许表示"未选中"状态。

4.3 封装判断方法

bool _isPointInPiece(Offset point, TangramPiece piece) {
  return _isPointInPolygon(point, piece.vertices);
}

将多边形判断封装为图块判断方法，提高了代码的可读性和可维护性。

五、拖拽系统

5.1 拖拽更新

在这里插入图片描述

void _handlePanUpdate(DragUpdateDetails details) {
  if (selectedPiece == null || dragStartPosition == null) return;

  final delta = details.localPosition - dragStartPosition!;

  setState(() {
    for (int i = 0; i < selectedPiece!.vertices.length; i++) {
      selectedPiece!.vertices[i] = selectedPiece!.vertices[i] + delta;
    }
    dragStartPosition = details.localPosition;
  });
}

计算拖拽偏移量，更新选中图块的所有顶点。通过更新所有顶点而不是使用变换矩阵，保持了代码的简单性。

5.2 拖拽结束

在这里插入图片描述

void _handlePanEnd(DragEndDetails details) {
  setState(() {
    selectedPiece = null;
    dragStartPosition = null;
  });
}

清除选择状态，准备下一次交互。这种设计让每次拖拽都是独立的操作。

六、旋转系统

在这里插入图片描述

6.1 旋转角度计算

void _rotateSelectedPiece(double angle) {
  if (selectedPiece == null) return;

  double centerX = 0, centerY = 0;
  for (var vertex in selectedPiece!.vertices) {
    centerX += vertex.dx;
    centerY += vertex.dy;
  }
  centerX /= selectedPiece!.vertices.length;
  centerY /= selectedPiece!.vertices.length;

  final center = Offset(centerX, centerY);

  setState(() {
    for (int i = 0; i < selectedPiece!.vertices.length; i++) {
      selectedPiece!.vertices[i] = _rotatePoint(
        selectedPiece!.vertices[i],
        center,
        angle,
      );
    }
  });
}

首先计算图块的几何中心（顶点平均值），然后围绕中心旋转所有顶点。这种旋转方式保持了图块的形状不变。

6.2 点旋转公式

Offset _rotatePoint(Offset point, Offset center, double angle) {
  final cosA = cos(angle);
  final sinA = sin(angle);

  final dx = point.dx - center.dx;
  final dy = point.dy - center.dy;

  return Offset(
    center.dx + dx * cosA - dy * sinA,
    center.dy + dx * sinA + dy * cosA,
  );
}

使用标准的2D旋转矩阵公式。先将点平移到原点，应用旋转矩阵，再平移回去。这是计算机图形学中的基本变换。

6.3 固定角度旋转

_buildControlButton('左转45°', Icons.rotate_left, () => _rotateSelectedPiece(-pi / 4)),
_buildControlButton('右转45°', Icons.rotate_right, () => _rotateSelectedPiece(pi / 4)),

提供45度的固定角度旋转。45度是90度的一半，便于对齐，且8次旋转正好回到原位。

七、翻转系统

7.1 水平翻转实现

void _flipSelectedPiece() {
  if (selectedPiece == null) return;

  double centerX = 0;
  for (var vertex in selectedPiece!.vertices) {
    centerX += vertex.dx;
  }
  centerX /= selectedPiece!.vertices.length;

  setState(() {
    for (int i = 0; i < selectedPiece!.vertices.length; i++) {
      selectedPiece!.vertices[i] = Offset(
        2 * centerX - selectedPiece!.vertices[i].dx,
        selectedPiece!.vertices[i].dy,
      );
    }
  });
}

围绕图块的几何中心X轴进行水平翻转，保持Y坐标不变。这种翻转对于平行四边形特别重要，因为它需要翻转才能拼出某些图案。

7.2 翻转数学原理

newX = 2 * centerX - oldX

镜像翻转公式的推导：

  • 点到中心的距离：d = oldX - centerX
  • 镜像点的距离：-d
  • 新坐标：centerX - d = centerX - (oldX - centerX) = 2 * centerX - oldX

八、几何图形类型

8.1 三角形系列

七巧板中有5个三角形：

  • 大三角形：底边4单位，高4单位，直角三角形
  • 中三角形：底边2单位，高2单位，直角三角形
  • 小三角形：底边1单位，高1单位，直角三角形

所有三角形都是等腰直角三角形，这种统一性使得它们可以组合成各种形状。

8.2 正方形

TangramPiece(
  id: 6,
  name: '正方形',
  vertices: [
    Offset(centerX, centerY),
    Offset(centerX + unitSize, centerY - unitSize),
    Offset(centerX + 2 * unitSize, centerY),
    Offset(centerX + unitSize, centerY + unitSize),
  ],
  color: Colors.blue.shade400,
),

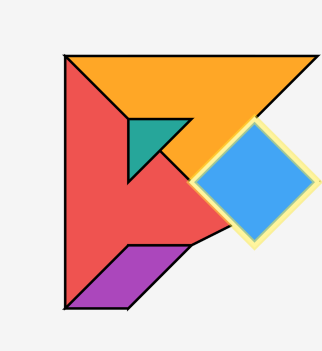
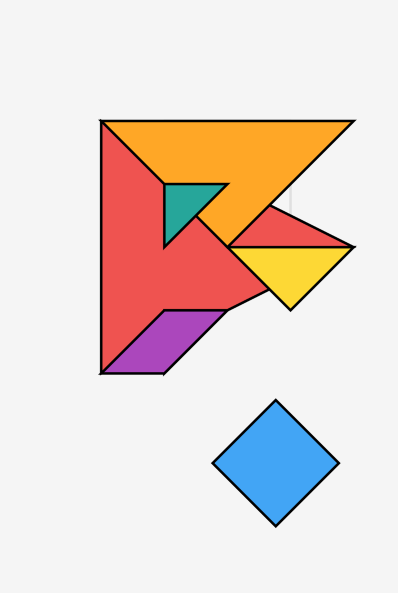
正方形旋转45度放置，边长为√2单位。四个顶点构成菱形布局，实际是正方形的旋转状态。

8.3 平行四边形

TangramPiece(
  id: 7,
  name: '平行四边形',
  vertices: [
    Offset(centerX - 2 * unitSize, centerY + 2 * unitSize),
    Offset(centerX - unitSize, centerY + 2 * unitSize),
    Offset(centerX, centerY + unitSize),
    Offset(centerX - unitSize, centerY + unitSize),
  ],
  color: Colors.purple.shade400,
),

平行四边形具有对边平行且相等的性质。这是七巧板中唯一不对称的图块，需要翻转功能才能充分发挥作用。

总结

本文详细介绍了七巧板游戏的几何图形和多边形碰撞检测系统。从数据结构设计到复杂的碰撞算法，从交互系统到数学变换，每个技术点都直接影响游戏的功能性和用户体验。通过这些技术的综合应用，实现了功能完整且交互流畅的七巧板游戏。

# flutter # 游戏 # harmonyos
Logo
开源鸿蒙跨平台开发者社区

开源鸿蒙跨平台开发社区汇聚开发者与厂商，共建“一次开发，多端部署”的开源生态，致力于降低跨端开发门槛，推动万物智联创新。

更多推荐

cover

Flutter for OpenHarmony 实战之基础组件：第二十九篇 Table 与 DataTable — 结构化数据展示专家

avatar 开源鸿蒙跨平台开发者社区
cover

Flutter for OpenHarmony 实战之基础组件：第二十八篇 LayoutBuilder 与 OrientationBuilder — 构建响应式鸿蒙应用

avatar 开源鸿蒙跨平台开发者社区
cover

Flutter for OpenHarmony 实战之基础组件：第三十一篇 Chip 系列组件 — 灵活的标签化交互

avatar 开源鸿蒙跨平台开发者社区