KMP算法详解

Next数组的本质：模式串前i+1个字符的最长公共前后缀长度，直接决定了失配后模式串指针的回退位置；双指针的核心作用：无论是构建Next数组还是正式匹配，双指针都实现了「一次遍历，不重复比较」，是时间复杂度优化到O(n+m)的关键；回退的核心原则：失配时主串指针不回退，仅模式串指针根据Next数组回退，跳过已验证的有效匹配部分；自匹配特性：构建Next数组时，模式串相当于自己和自己匹配，复用了KM

ztking666

124人浏览 · 2026-01-30 13:18:00

ztking666 · 2026-01-30 13:18:00 发布

KMP算法是一种高效的字符串匹配算法
解决了暴力算法冗杂繁琐的特点
将时间复杂度从n^2优化到了n+m(子串和模式串长度)

其核心思想是：匹配失配时，模式串指针不回退到起点，而是根据预处理的Next数组回退到「合适位置」，跳过已匹配的有效部分，避免重复比较。

一、回退机制

你有两个字符串

主串（Text, S）：ABABABCABA
模式串（Pattern, P）：ABABC
匹配过程：二者逐字符匹配，当匹配到模式串的C时，对应主串的第三个A，此时失配；已成功匹配的字符为ABAB。
优化操作：找到已匹配部分ABAB的最长相等前后缀（AB），让模式串的前缀AB直接匹配主串的后缀AB，模式串指针回退到该前缀的末尾，主串指针不回退，继续向后匹配。
总而言之就是
当失配的时候用模式串的前缀末尾继续去匹配子串的后缀末尾

关键概念

前缀：字符串中除最后一个字符外，所有以第一个字符开头的连续子串（如ABAB的前缀：A、AB、ABA）；
后缀：字符串中除第一个字符外，所有以最后一个字符结尾的连续子串（如ABAB的后缀：B、AB、BAB）；
最长公共前后缀：前缀和后缀中长度最长且内容完全相等的子串（如ABAB的最长公共前后缀为AB）。

二、Next数组

KMP的回退机制完全由Next数组实现，Next数组是为模式串单独构建的数组，与模式串长度一致，数组中每个位置的值对应：模式串当前位置字符失配时，指针应回退的目标索引（本质是模式串前i个字符的最长公共前后缀长度）。
Next数组长度与模式串一一对应除了第一个值进行的初始化,
其他元素例存储了当前对应长度的最长公共前后缀的大小,也就是失配后应该跳转的索引
在这里插入图片描述

简单来说：Next[i] 表示模式串前i+1个字符的最长公共前后缀的长度，也是失配后模式串指针应回退到的位置。

三、KMP算法实现（Java）

KMP算法分为两个核心步骤：构建Next数组、利用Next数组进行主串与模式串的匹配，整体采用双指针法实现，且构建Next数组的过程也复用了KMP的核心思想（模式串自匹配）。

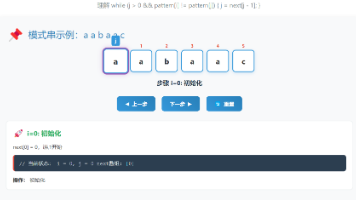
步骤1：构建Next数组

核心逻辑
用双指针分别指向模式串的前缀末尾（j）和后缀末尾（i），通过自匹配找到每个位置的最长公共前后缀长度，填充Next数组：

j：既代表前缀末尾位置，也代表当前已匹配的最长公共前后缀长度，初始为0；
i：代表后缀末尾位置，从1开始遍历（第一个字符无前后缀，Next[0]固定为0）；
失配回退：前后缀字符不匹配时，j根据已构建的Next数组回退一格（j = next[j-1]），直到j=0或字符匹配；
匹配更新：前后缀字符匹配时，j自增（最长公共前后缀长度+1），并将j赋值给Next[i]。

回退机制和KMP算法的后退机制是一样的,本质上就是通过营造时间差
自己和自己匹配
这个因为在构造Next数组中的时候,前面的Next数组已经构建完毕了,这样就可以使用该思想了

代码实现

/**
 * 构建模式串的Next数组
 * @param pattern 模式串
 * @return 对应Next数组
 */
public static int[] getNext(String pattern) {
    int m = pattern.length();
    int[] next = new int[m];
    next[0] = 0; // 第一个字符无前后缀，最长公共前后缀长度为0
    
    // j：前缀末尾/已匹配长度，i：后缀末尾
    for (int i = 1, j = 0; i < m; i++) {
        // 失配回退：利用已构建的Next数组，回退到合适位置
        while (j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
            j = next[j - 1];
        }
        // 匹配成功：最长公共前后缀长度+1
        if (pattern.charAt(i) == pattern.charAt(j)) {
            j++;
        }
        // 填充当前位置的Next值
        next[i] = j;
    }
    return next;
}

步骤2：利用Next数组进行字符串匹配

核心逻辑
用双指针分别指向主串（i）和模式串（j），逐字符匹配，失配时通过Next数组让模式串指针回退，主串指针始终不回退：

i：主串遍历指针，从0开始，一直向后遍历不回退；
j：模式串匹配指针，从0开始，匹配成功则后移，失配则根据Next数组回退；
失配处理：主串与模式串字符不匹配时，j回退（j = next[j-1]），直到j=0或字符匹配；
匹配成功判定：当j等于模式串长度时，说明模式串完全匹配，返回主串中匹配的起始索引；
边界检查：提前判断模式串为空、主串长度小于模式串的情况，直接返回对应结果。

代码实现
import java.util.Arrays;
/**
 * KMP核心匹配方法
 * @param text 主串
 * @param pattern 模式串
 * @return 模式串在主串中首次匹配的起始索引，未找到返回-1
 */
public static int kmpSearch(String text, String pattern) {
    // 边界检查：模式串为空直接返回0，主串更短直接返回-1
    if (pattern == null || pattern.length() == 0) return 0;
    if (text == null || text.length() < pattern.length()) return -1;

    int n = text.length(); // 主串长度
    int m = pattern.length(); // 模式串长度
    int[] next = getNext(pattern); // 获取模式串的Next数组
    // System.out.println("Next数组：" + Arrays.toString(next)); // 调试用，打印Next数组

    // i：主串指针，j：模式串指针
    for (int i = 0, j = 0; i < n; i++) {
        // 失配回退：利用Next数组跳过重复匹配部分
        while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
            j = next[j - 1];
        }
        // 匹配成功：模式串指针后移
        if (text.charAt(i) == pattern.charAt(j)) {
            j++;
        }
        // 完全匹配：返回起始索引（当前主串位置 - 模式串长度 + 1）
        if (j == m) {
            return i - m + 1;
            // 若需查找所有匹配位置，注释上方return，执行以下代码：
            // j = next[j - 1]; // 回退继续匹配
            // res.add(i - m + 1); // 收集起始索引
        }
    }
    return -1; // 未找到匹配
}