KMP算法详解：从原理到实现

建议先看一下算法问题精讲之字符串，打一下基础
“本系列会一直更新下去，可否给个关注呢”

一、问题引入：字符串匹配问题

在字符串处理中，一个常见的问题是：如何在文本串 text 中查找模式串 pattern 是否出现？这就是字符串匹配问题。

1.1 朴素匹配算法

最简单的思路是暴力匹配：

bool naiveSearch(string text, string pattern) {
    int n = text.length();
    int m = pattern.length();
    
    for (int i = 0; i <= n - m; i++) {
        int j = 0;
        while (j < m && text[i + j] == pattern[j]) {
            j++;
        }
        if (j == m) return true;
    }
    return false;
}

时间复杂度：O(m×n)，效率低下。

1.2 一个实际场景

假设我们要在 DNA 序列 "ATCGTAGCTAGCTAGCT" 中寻找 "TAGCT"，朴素算法会进行很多不必要的比较。

---

二、KMP算法核心思想

KMP（Knuth-Morris-Pratt）算法的核心是：利用已经匹配的部分信息，避免回溯主串指针。

2.1 关键观察

当匹配失败时，模式串中已经匹配的部分可能包含有助于继续匹配的信息。

例子：

文本串:    a b c a b c d e f g
模式串:    a b c a b d
                ↑ 此处失败
已匹配:     a b c a b

在位置5匹配失败时（'c' ≠ 'd'），我们注意到已匹配的 "abcab" 有相同的前后缀 "ab"，因此可以跳过一些比较。

2.2 前缀函数（Prefix Function）

定义 next[i] 为模式串 P[0..i] 的最长相等真前后缀长度。

什么是真前后缀？

• 真前缀：从开头开始但不包含整个字符串的连续子串
• 真后缀：以当前位置结束但不包含整个字符串的连续子串

示例："abab" 的 next[3]

字符串: a b a b
下标:   0 1 2 3

真前缀: "a", "ab", "aba"
真后缀: "b", "ab", "bab"

相等前后缀: "ab"（长度2）
所以 next[3] = 2

---

三、KMP算法详细步骤

3.1 构建next数组

vector<int> buildNext(string pattern) {
    int m = pattern.length();
    vector<int> next(m, 0);
    
    for (int i = 1, j = 0; i < m; i++) {
        // 不匹配时回退
        while (j > 0 && pattern[i] != pattern[j]) {
            j = next[j - 1];
        }
        // 匹配成功
        if (pattern[i] == pattern[j]) {
            j++;
        }
        next[i] = j;
    }
    return next;
}

3.2 理解回退操作

while (j > 0 && pattern[i] != pattern[j]) { j = next[j - 1]; }

这是一个关键点！当匹配失败时，我们不是回到开头，而是回到已匹配部分的最长相等前后缀的位置。

例子：构建 "aabaac" 的next数组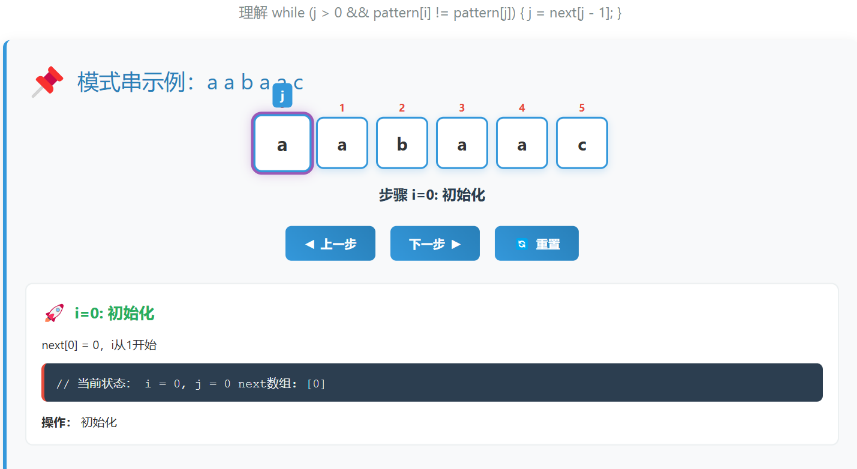

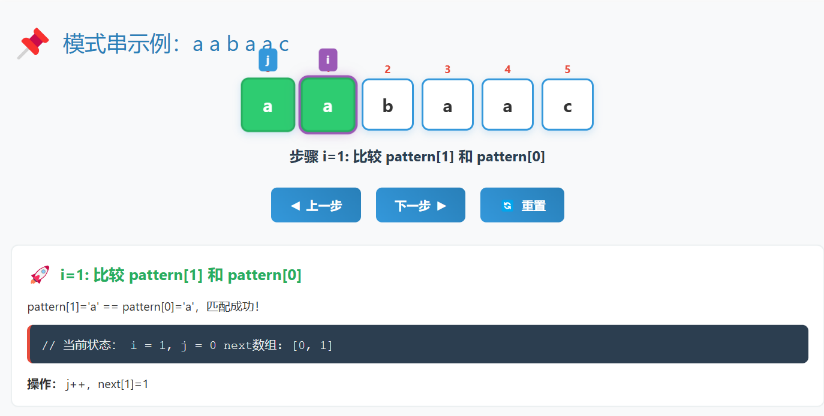
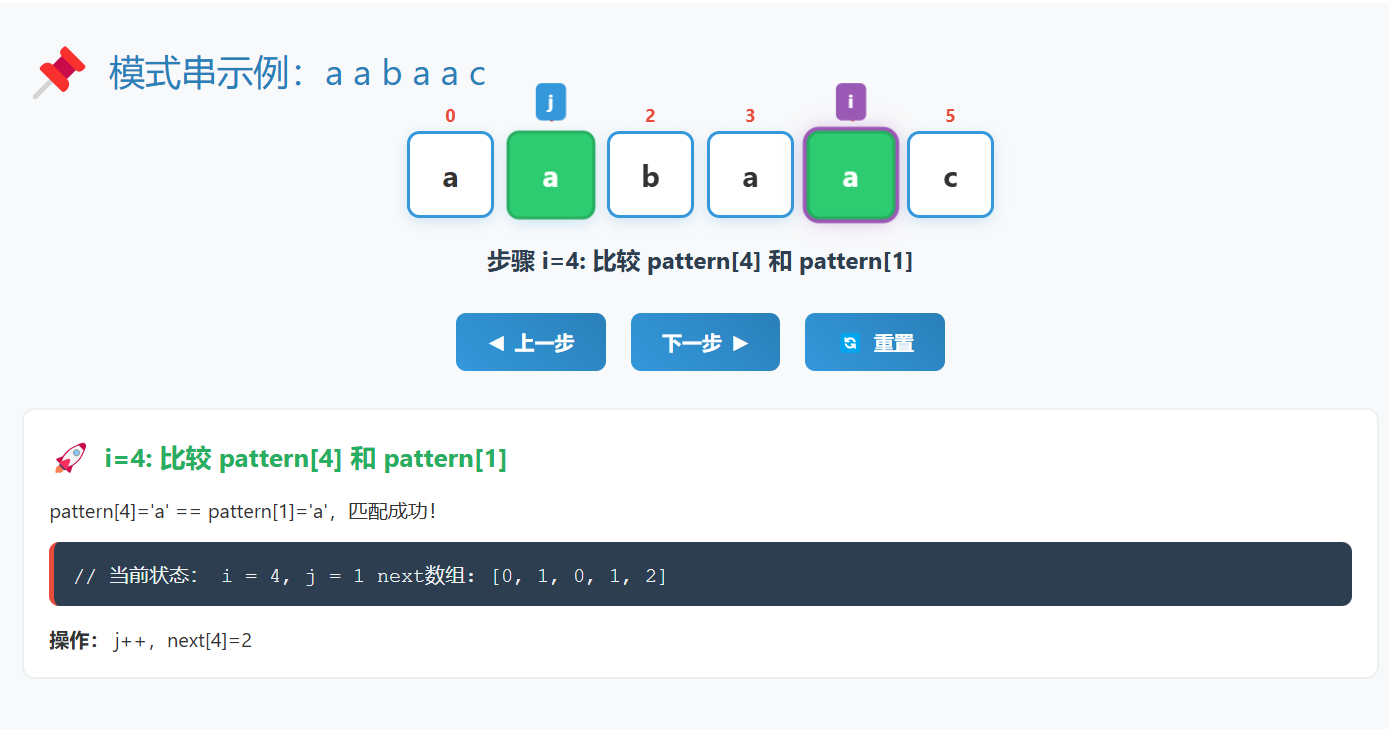
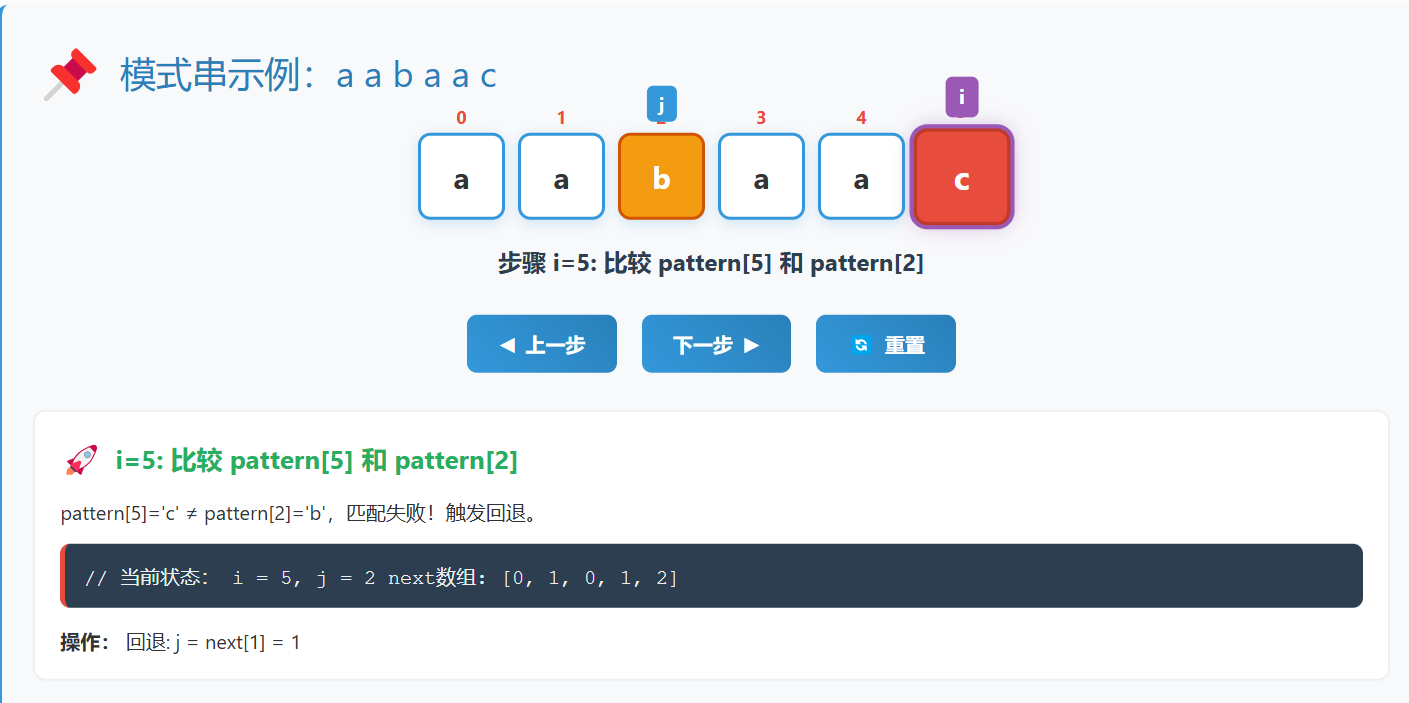
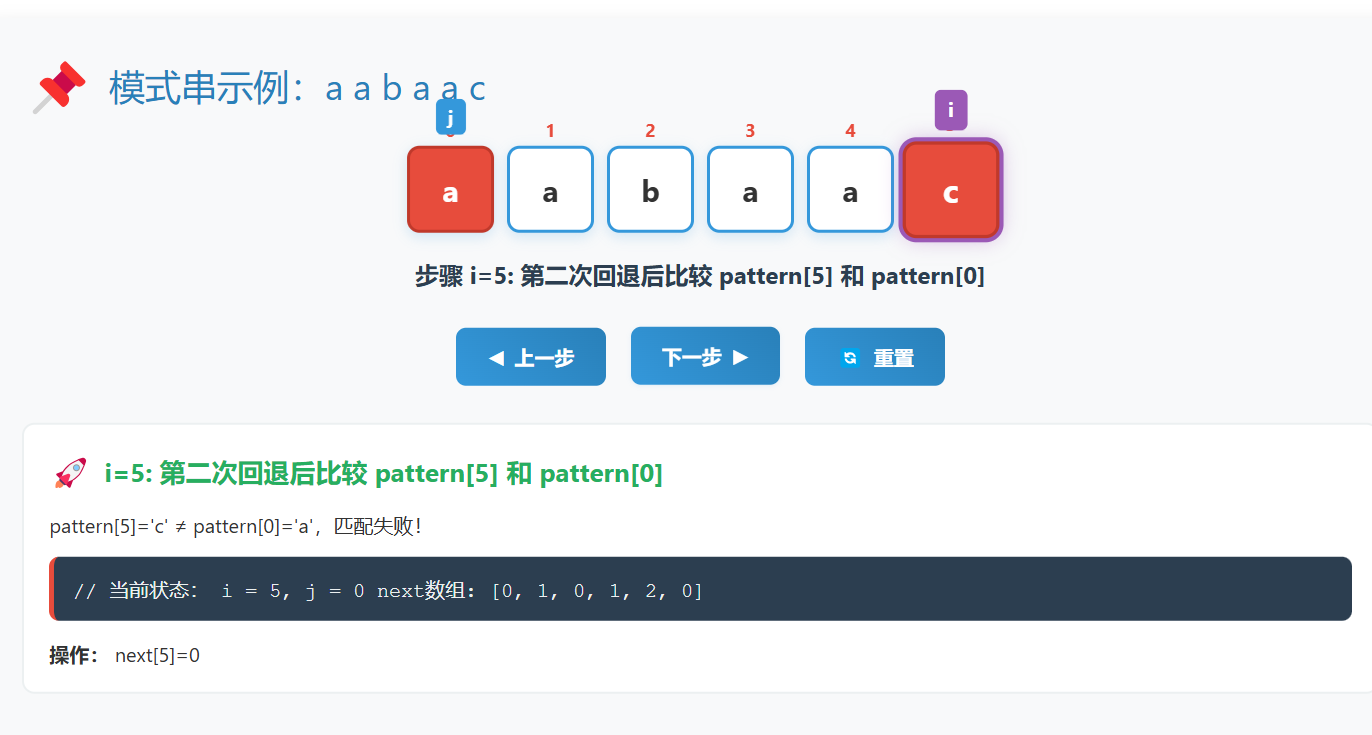
3.3 搜索过程

bool kmpSearch(string text, string pattern) {
    int n = text.length();
    int m = pattern.length();
    
    if (m == 0) return true;
    if (n < m) return false;
    
    vector<int> next = buildNext(pattern);
    int j = 0;  // 模式串指针
    
    for (int i = 0; i < n; i++) {
        while (j > 0 && text[i] != pattern[j]) {
            j = next[j - 1];  // 回退
        }
        if (text[i] == pattern[j]) {
            j++;
        }
        if (j == m) {
            return true;  // 找到匹配
        }
    }
    return false;
}

---

四、KMP算法应用实例

4.1 重复子串问题

判断字符串 s 是否可由某个子串重复多次构成。

核心公式：

bool repeatedSubstringPattern(string s) {
    int n = s.length();
    vector<int> next(n, 0);
    
    // 构建next数组
    for (int i = 1, j = 0; i < n; i++) {
        while (j > 0 && s[i] != s[j]) {
            j = next[j - 1];
        }
        if (s[i] == s[j]) {
            j++;
        }
        next[i] = j;
    }
    
    int len = n - next[n - 1];
    return next[n - 1] > 0 && n % len == 0;
}

原理：

• 如果 s 由长度为 len 的子串重复 k 次构成
• 则 next[n-1] = n - len
• 所以 len = n - next[n-1]
• 需要满足 n % len == 0

示例：

• "abab": n=4, next[3]=2, len=2, 4%2=0 → true
• "aba": n=3, next[2]=1, len=2, 3%2≠0 → false

4.2 旋转字符串问题

判断字符串 goal 是否可通过旋转 s 得到。

巧妙解法：

bool rotateString(string s, string goal) {
    if (s.length() != goal.length()) return false;
    
    // 关键：s + s 包含了所有可能的旋转结果
    string t = s + s;
    
    // 使用KMP判断goal是否是t的子串
    return kmpSearch(t, goal);
}

原理：

• 将 s 旋转得到的字符串一定是 s + s 的子串
• 例如：s = "abcde", 旋转得到 "cdeab"
• s + s = "abcdeabcde" 包含 "cdeab"

---

五、时间复杂度分析

算法	预处理时间	匹配时间	总时间
朴素算法	O(1)	O(m×n)	O(m×n)
KMP算法	O(m)	O(n)	O(m+n)

• 构建next数组：O(m)，每个字符最多被比较两次
• 搜索过程：O(n)，主串指针不回溯
• 总复杂度：O(m+n)

---

六、常见误区与技巧

6.1 理解next数组的物理意义

next[i] 不是简单的"失败时跳转到哪里"，而是"当前位置匹配失败时，已匹配部分中可重复利用的最大长度"。

6.2 空字符串和单字符的处理

• 空模式串匹配任何文本串
• 单字符模式串退化到朴素匹配

6.3 优化空间

如果只判断是否匹配而不需要所有位置，可以边构建next数组边匹配。

---

七、总结

KMP算法通过前缀函数避免了文本串指针的回溯，将字符串匹配的时间复杂度从O(m×n)降低到O(m+n)。虽然理解起来有一定难度，但掌握其核心思想对解决字符串相关问题大有裨益。

记忆要点：

1. 理解真前后缀的概念
2. 掌握next数组的构建过程
3. 理解回退操作的原理
4. 学会应用到实际问题

---