详解KMP算法的原理和代码实现
连接, 拆分之后特殊字符消失,因为拆分之前两个字符串直接使用。, 如果不相等继续找第三长的。那么问题就变成了, 如何根据。的思想, 假设已经计算出了。, 对新的字符串求一遍。对于当前情况, 如果。, 可以进行拼接操作。
算法能解决的问题
给定模式串 p p p和主串 s s s, 检查 s s s中是否存在 p p p串, 并且检查 p p p串出现的位置
算法原理
- 假设给定字符串 s = A C A A C A s = ACAACA s=ACAACA
- 将不包含自身的前后缀列出, 找到最长的相等的前后缀, 也就是最长匹配真前后缀, 长度记为 π i \pi_i πi
- 然后将字符串的所有非空前缀全部列出来
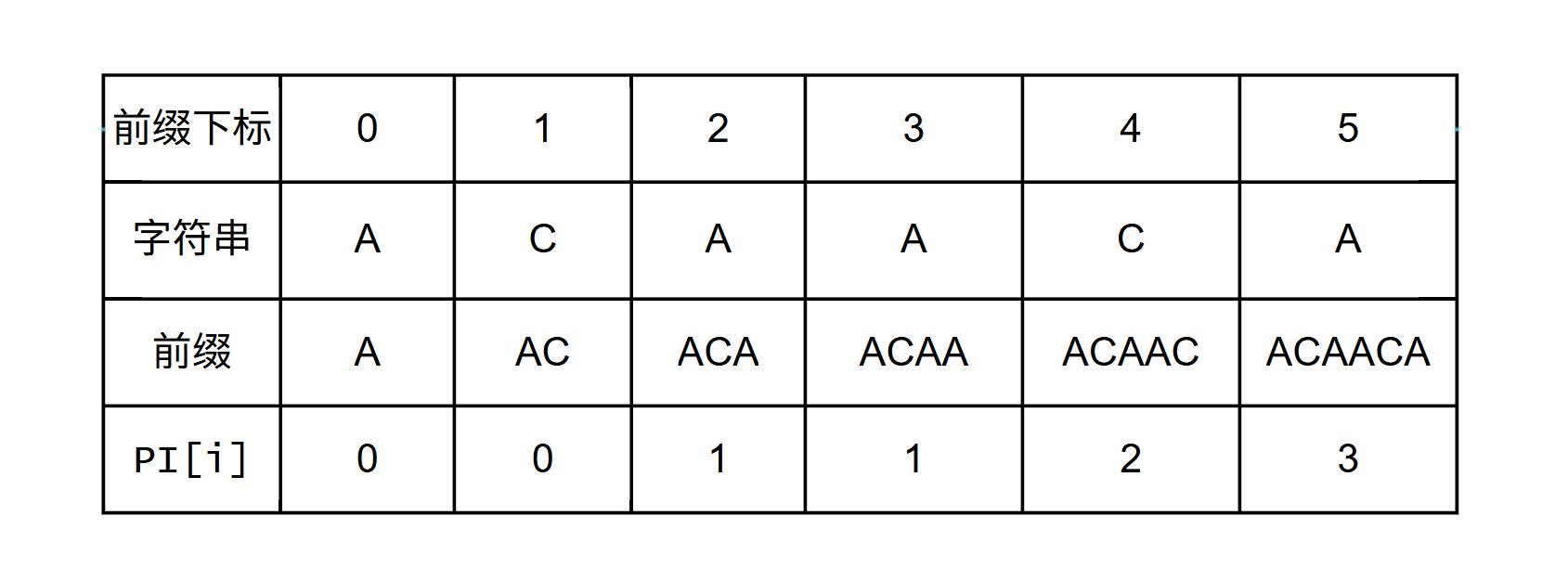
如果直接暴力求 π \pi π, 算法时间复杂度 O ( n 2 ) O(n ^ 2) O(n2), 需要进行优化
用递推的思想, 假设已经计算出了 π 0 ∼ π i − 1 \pi_{0} \sim \pi_{i - 1} π0∼πi−1, 当前希望计算 π i \pi_{i} πi
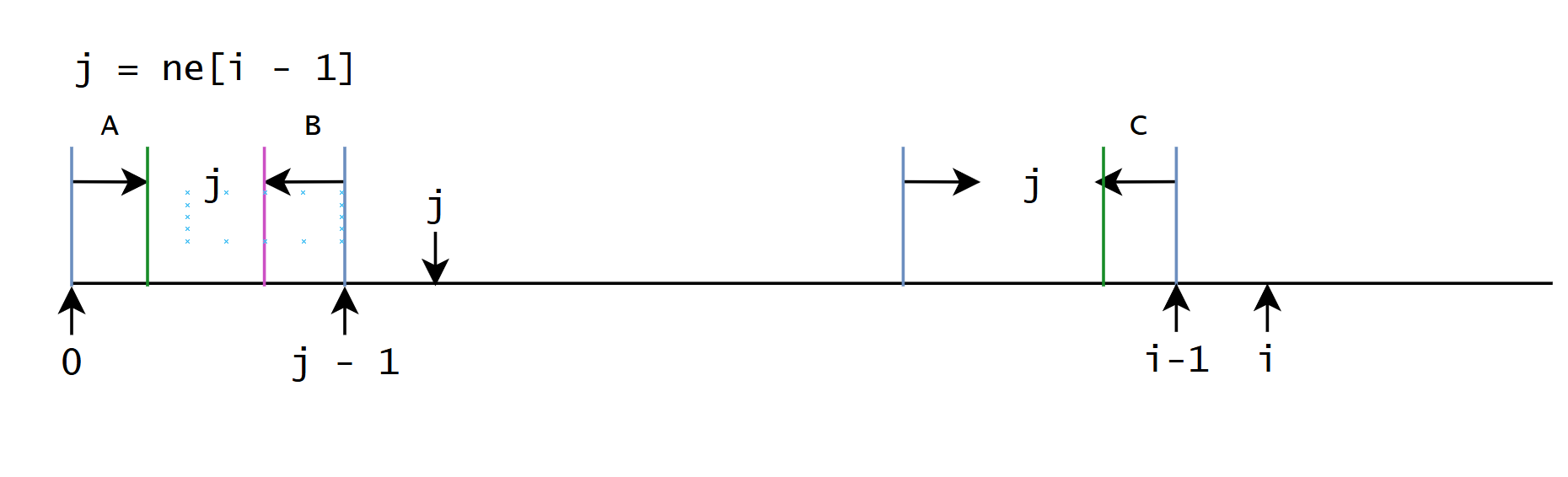
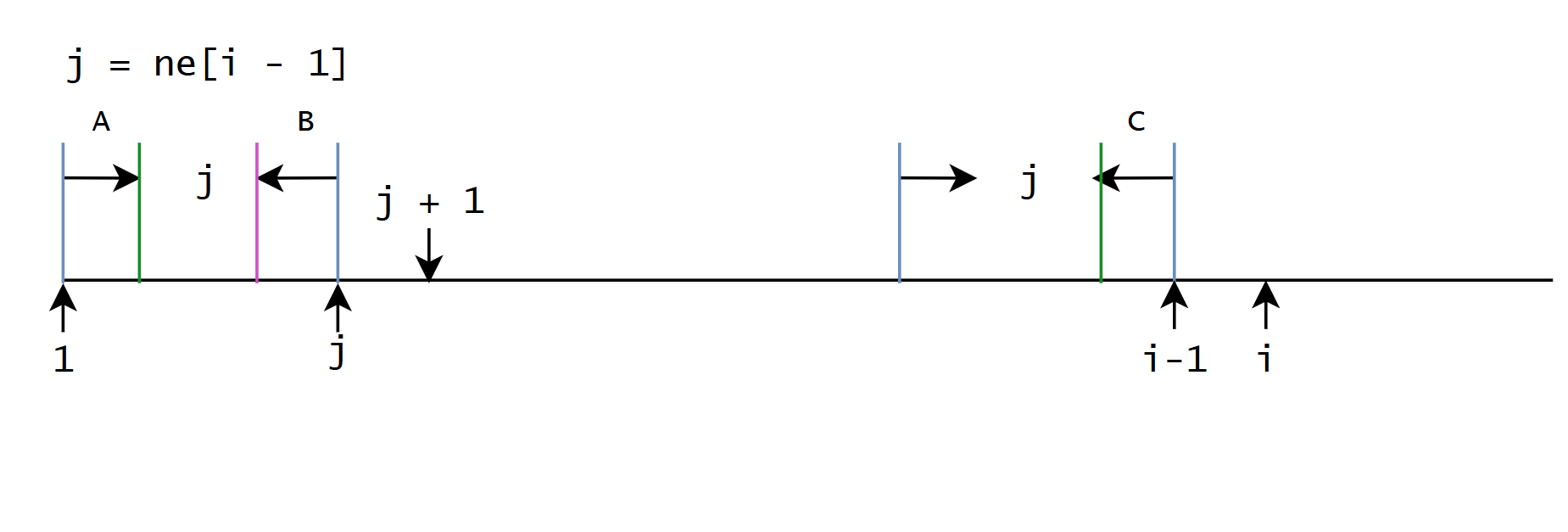
令 j = π i − 1 j = \pi _{i - 1} j=πi−1
对于当前情况, 如果 S [ j ] = S [ i ] S[j] = S[i] S[j]=S[i], 那么 π i = π i − 1 + 1 \pi_{i} = \pi_{i - 1} + 1 πi=πi−1+1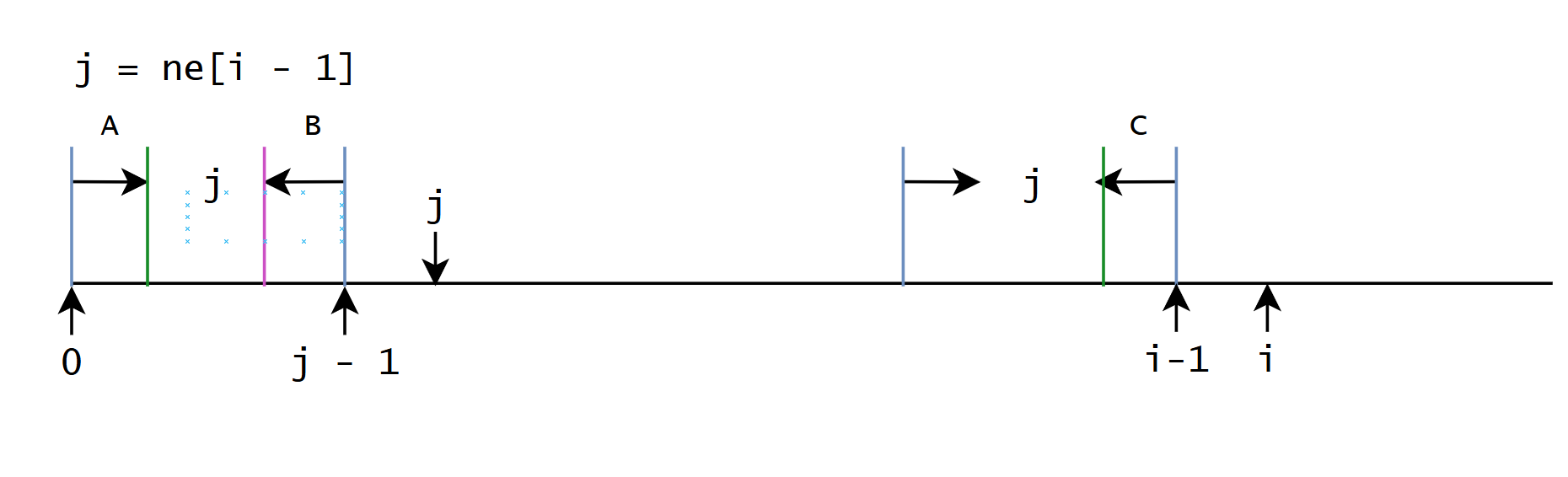
如果不相等, 找第二长的公共前后缀, 假设位置是 t t t, 如果相等 π i = π t + 1 \pi_{i} = \pi_{t} + 1 πi=πt+1, 如果不相等继续找第三长的
那么问题就变成了, 如何根据当前最长后缀找到第二长的前缀
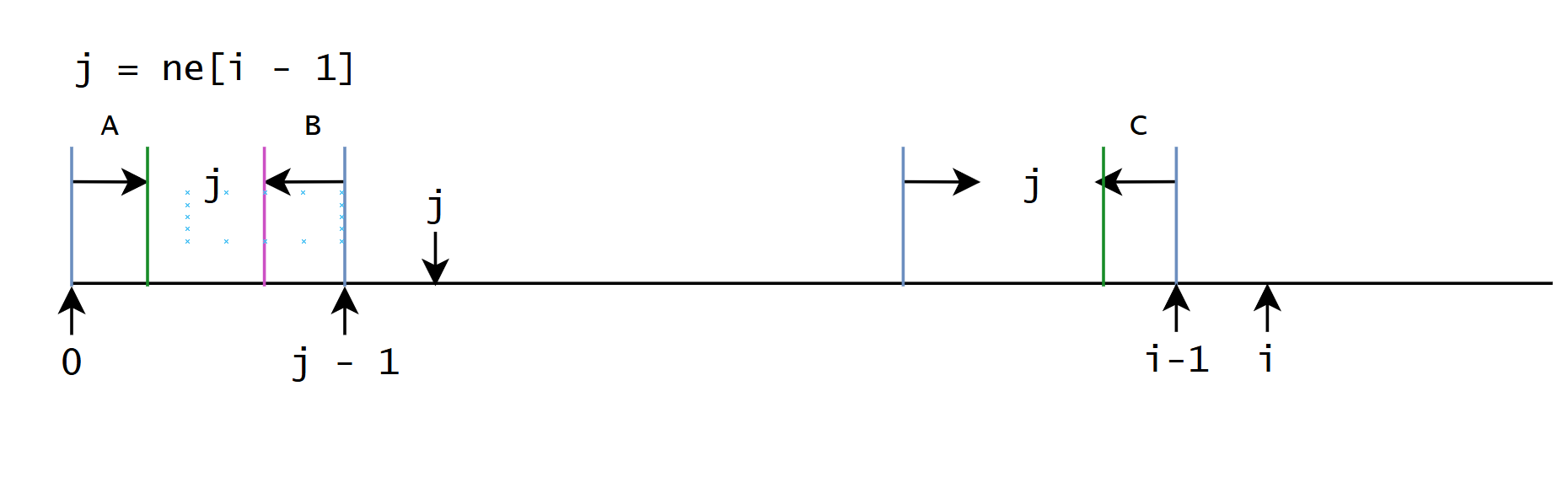
A , B , C A, B, C A,B,C三段相等, 也就是
int j = ne[i - 1];
if (s[j] != s[i]) {
j = ne[j - 1];
}
这样就可以在线性的时间复杂度内处理出 π i \pi_{i} πi数组
那么如何使用 π i \pi_{i} πi来解决字符串匹配的问题?
假设目标串是 S S S, 给定的模式串是 P P P, 可以进行拼接操作S' = P + # + S, 对新的字符串求一遍 π i \pi_{i} πi, 当 π i = P . s i z e ( ) \pi_{i} = P.size() πi=P.size(), 说明找到了模式串
为什么拆分写法需要将指针 j j j清零?
- 实际上拼接字符串过程中的添加的特殊字符就是在 i i i遍历到 S S S串的时候, j j j需要重新指向 P P P串的第一个前缀位置进行比对(主串可以理解为后缀)
- 如果不将 j j j指针清零, 相当于模式串和主串直接拼接, 假设某一段模式串 + 某一段主串匹配上了某一段模式串的前缀, 这实际是违法的
- 总结来说, 将 j j j指针清零相当于告诉
ne数组, 后面不会再有更长的最长匹配真前后缀, 需要从头开始重新匹配, 这样符合我们希望将 p p p串作为前缀, s s s串作为后缀的需求, 因此需要将 j j j指针清零
算法步骤
- 根据
int j = ne[i - 1]构建出ne数组 - 将模式串拼接到主串, 假设新的字符串是 s ′ s' s′, 在拼接后发现最长匹配真后缀的长度和模式串 p p p相等, 相当于找到了模式串
- 如果不将模式串拼接到主串, 可以直接遍历主串, 但是需要将
j = ne[i - 1]的j指针指向开头
例题
从原理出发的写法
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
class Solution {
public:
int strStr(string haystack, string needle) {
int m = needle.size();
int ne[N] = {0};
string new_s = needle + '@' + haystack;
for (int i = 1; i < new_s.size(); ++i) {
int j = ne[i - 1];
while (j && new_s[j] != new_s[i]) j = ne[j - 1];
if (new_s[j] == new_s[i]) ne[i] = j + 1;
if (ne[i] == m) {
return i - 2 * m;
}
};
return -1;
}
};
拆分写法
因为拆分之前两个字符串直接使用特殊字符连接, 拆分之后特殊字符消失, j j j需要清零, 特殊字符的作用就是将 j j j移动到初始位置
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
class Solution {
public:
int strStr(string s, string p) {
int n = s.size(), m = p.size();
int ne[N] = {0};
for (int i = 1; i < m; ++i) {
int j = ne[i - 1];
while (j && p[j] != p[i]) j = ne[j - 1];
if (p[j] == p[i]) ne[i] = j + 1;
}
for (int i = 0, j = 0; i < n; ++i) {
while (j && p[j] != s[i]) j = ne[j - 1];
if (p[j] == s[i]) j++;
if (j == m) return i - m + 1;
}
return -1;
}
};
最普遍的模板写法
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
class Solution {
public:
int strStr(string s, string p) {
s = ' ' + s, p = ' ' + p;
int n = s.size(), m = p.size();
int ne[N] = {0};
for (int i = 2; i < m; ++i) {
int j = ne[i - 1];
while (j && p[j + 1] != p[i]) j = ne[j];
if (p[j + 1] == p[i]) ne[i] = j + 1;
}
for (int i = 1, j = 0; i < n; ++i) {
while (j && p[j + 1] != s[i]) j = ne[j];
if (p[j + 1] == s[i]) j++;
if (j == m - 1) return i - m + 1;
}
return -1;
}
};
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)