欢迎加入开源鸿蒙跨平台社区：开源鸿蒙跨平台开发者社区

Flutter for OpenHarmony 进阶：递归算法与数学证明深度解析

摘要

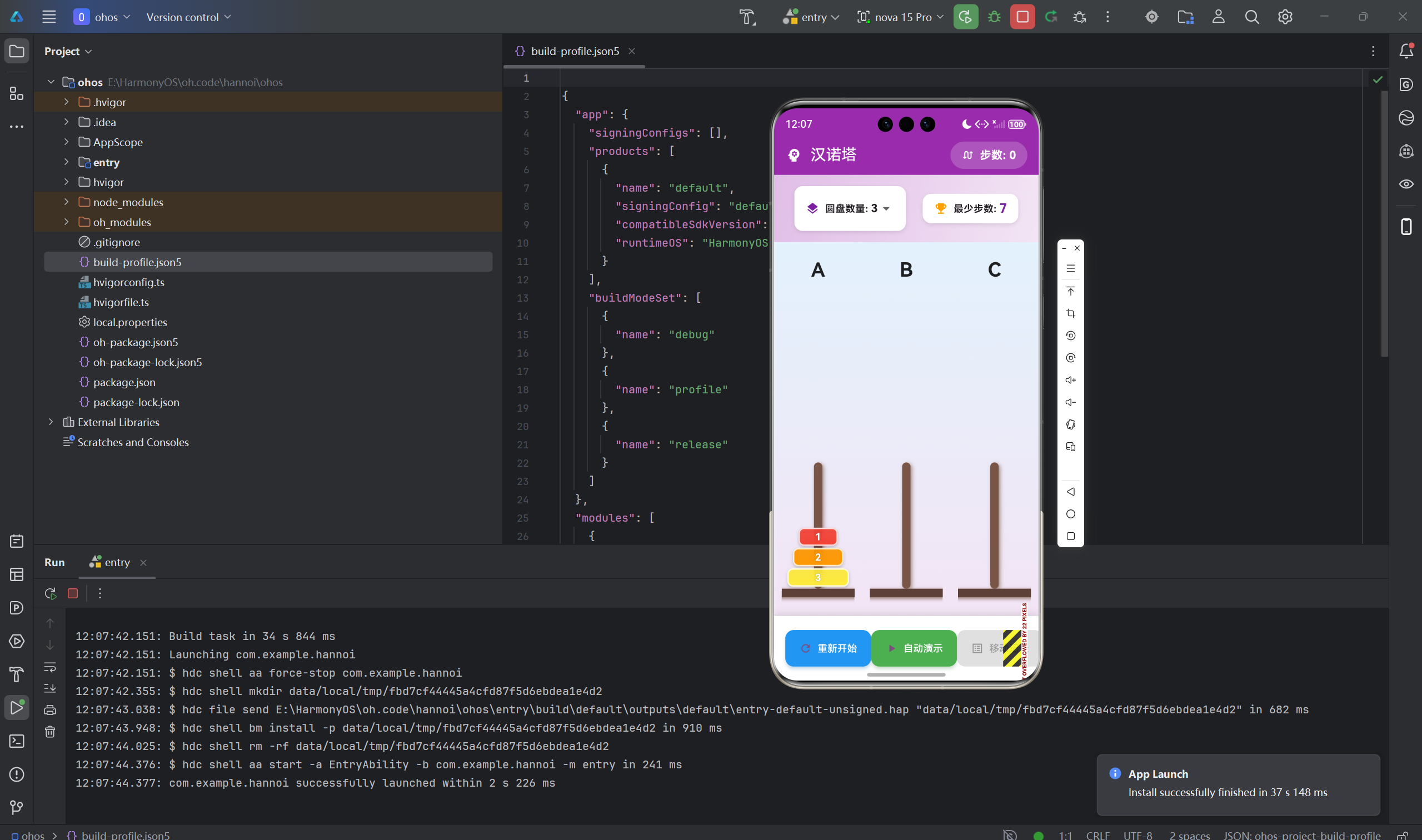
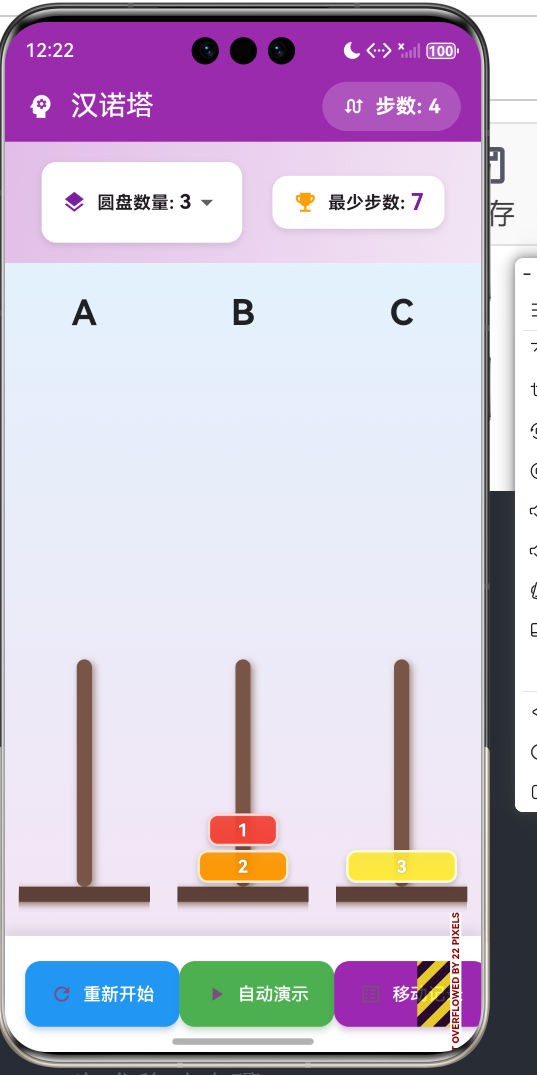
汉诺塔是学习递归算法的经典案例，其优雅的数学性质和简洁的算法实现使其成为计算机科学教育的重要内容。本文深入讲解汉诺塔问题的数学原理、递归算法分析、迭代解法、算法优化等高级技术点。通过本文学习，读者将深入理解递归思想，掌握算法复杂度分析方法，了解如何将递归算法转化为迭代实现。

---

一、数学原理

1.1 问题定义

汉诺塔问题由法国数学家Édouard Lucas在1883年发明：

• 目标：将n个圆盘从源塔移到目标塔
• 规则：
  1. 一次只能移动一个圆盘
  2. 大圆盘不能放在小圆盘上面
  3. 可以使用辅助塔

1.2 最少移动次数

定理：n个圆盘需要的最少移动次数是 2^n - 1

证明：

基础情况：

• n = 1：需要1次移动 = 2^1 - 1 ✓

归纳假设：
假设对于n = k，最少移动次数是 2^k - 1

归纳步骤：
对于n = k + 1：

1. 将k个圆盘从源塔移到辅助塔：2^k - 1次
2. 将第k+1个圆盘从源塔移到目标塔：1次
3. 将k个圆盘从辅助塔移到目标塔：2^k - 1次

总计：2 × (2^k - 1) + 1 = 2^(k+1) - 1 ✓

1.3 数列分析

移动次数构成数列：1, 3, 7, 15, 31, 63, 127…

通项公式：a_n = 2^n - 1

递推关系：a_n = 2 × a_(n-1) + 1

生成函数：G(x) = x / (1 - 2x - x²)

---

二、递归算法深度分析

2.1 递归树分析

以n=3为例的递归调用树：

hanoi(3, A, C, B)
├── hanoi(2, A, B, C)
│   ├── hanoi(1, A, C, B) → [A→C]
│   ├── [A→B]
│   └── hanoi(1, C, B, A) → [C→B]
├── [A→C]
└── hanoi(2, B, C, A)
    ├── hanoi(1, B, A, C) → [B→A]
    ├── [B→C]
    └── hanoi(1, A, C, B) → [A→C]

移动序列：A→C, A→B, C→B, A→C, B→A, B→C, A→C

对应代码实现：

// 汉诺塔递归算法
void _hanoi(int n, String source, String target, String auxiliary, List<List<String>> moves) {
  if (n == 1) {
    moves.add([source, target]);
    return;
  }

  // 将 n-1 个圆盘从源塔移到辅助塔
  _hanoi(n - 1, source, auxiliary, target, moves);

  // 将最大的圆盘从源塔移到目标塔
  moves.add([source, target]);

  // 将 n-1 个圆盘从辅助塔移到目标塔
  _hanoi(n - 1, auxiliary, target, source, moves);
}

2.2 递归方程

T(n) = 2×T(n-1) + 1,  T(1) = 1

求解：

T(n) = 2×T(n-1) + 1
     = 2×(2×T(n-2) + 1) + 1
     = 4×T(n-2) + 2 + 1
     = 4×(2×T(n-3) + 1) + 2 + 1
     = 8×T(n-3) + 4 + 2 + 1
     = ...
     = 2^n × T(0) + Σ(2^i), i从0到n-1
     = 2^n - 1

2.3 栈空间分析

递归调用的栈空间：

递归深度 = n
栈空间 = O(n)

每次递归调用需要保存：
- 局部变量
- 返回地址
- 参数

总空间复杂度：O(n)

---

三、动画执行与状态管理

3.1 自动求解实现

// 自动求解（递归算法）
void _autoSolve() {
  if (_isSolving) return;

  setState(() {
    _isSolving = true;
  });

  // 重置游戏
  _initGame();

  // 生成移动步骤
  final moves = <List<String>>[];
  _hanoi(_diskCount, _source.name, _target.name, _auxiliary.name, moves);

  // 执行移动动画
  _executeMoves(moves, 0);
}

// 执行移动动画
void _executeMoves(List<List<String>> moves, int index) {
  if (index >= moves.length) {
    setState(() {
      _isSolving = false;
    });
    return;
  }

  final fromName = moves[index][0];
  final toName = moves[index][1];

  final from = _getTowerByName(fromName);
  final to = _getTowerByName(toName);

  if (from != null && to != null) {
    final disk = from.pop();
    to.push(disk);
    _moveCount++;
    _moveLog.add('将圆盘 ${disk.size} 从 $fromName 移到 $toName');

    setState(() {});

    // 继续下一步
    _animationTimer = Timer(const Duration(milliseconds: 500), () {
      _executeMoves(moves, index + 1);
    });
  }
}

// 根据名称获取塔
Tower? _getTowerByName(String name) {
  switch (name) {
    case 'A':
      return _source;
    case 'B':
      return _auxiliary;
    case 'C':
      return _target;
    default:
      return null;
  }
}

// 停止自动求解
void _stopSolving() {
  _animationTimer?.cancel();
  setState(() {
    _isSolving = false;
  });
}

3.2 状态管理

class _GamePageState extends State<GamePage> {
  // 三座塔
  late Tower _source;
  late Tower _auxiliary;
  late Tower _target;

  // 圆盘数量
  int _diskCount = 3;

  // 移动次数
  int _moveCount = 0;

  // 是否正在自动求解
  bool _isSolving = false;

  // 选中的塔（用于点击移动）
  Tower? _selectedTower;

  // 移动记录
  final List<String> _moveLog = [];

  // 动画控制器
  Timer? _animationTimer;

  @override
  void dispose() {
    _animationTimer?.cancel();
    super.dispose();
  }
}

---

四、迭代解法

4.1 为什么需要迭代解法

递归解法的问题：

1. 栈溢出风险（n很大时）
2. 无法随时暂停/恢复
3. 难以保存中间状态

4.2 二进制表示法

汉诺塔的解法与二进制有奇妙的联系：

void hanoiIterative(int n, String source, String target, String auxiliary) {
  final totalMoves = (1 << n) - 1;

  // 如果n是偶数，交换辅助塔和目标塔
  if (n % 2 == 0) {
    final temp = target;
    target = auxiliary;
    auxiliary = temp;
  }

  for (int move = 1; move <= totalMoves; move++) {
    final from = _getPeg(n, move, source, target, auxiliary);
    final to = _getOtherPeg(n, move, source, target, auxiliary, from);

    print('Move $move: $from -> $to');
    _moveDisk(from, to);
  }
}

int _getPeg(int n, int move, String source, String target, String auxiliary) {
  // 使用格雷码确定移动
  int xor = move & (move - 1);
  int bitPos = 0;
  while (xor > 0) {
    xor >>= 1;
    bitPos++;
  }

  int disk = bitPos % n;
  return _getDiskPosition(disk, source, target, auxiliary);
}

String _getDiskPosition(int disk, String source, String target, String auxiliary) {
  // 根据圆盘位置确定从哪个塔移动
  // 这里需要跟踪每个圆盘的位置
  // 简化实现，实际需要维护圆盘位置数组
  return source;
}

4.3 栈模拟递归

class HanoiState {
  final int n;
  final String source;
  final String target;
  final String auxiliary;
  final int stage;  // 0-开始, 1-第一次递归后, 2-第二次递归后

  HanoiState({
    required this.n,
    required this.source,
    required this.target,
    required this.auxiliary,
    required this.stage,
  });

  HanoiState copyWith({int? n, String? source, String? target, String? auxiliary, int? stage}) {
    return HanoiState(
      n: n ?? this.n,
      source: source ?? this.source,
      target: target ?? this.target,
      auxiliary: auxiliary ?? this.auxiliary,
      stage: stage ?? this.stage,
    );
  }
}

void hanoiIterative(int n, String source, String target, String auxiliary) {
  final stack = <HanoiState>[];
  stack.add(HanoiState(
    n: n,
    source: source,
    target: target,
    auxiliary: auxiliary,
    stage: 0,
  ));

  while (stack.isNotEmpty) {
    final state = stack.removeLast();

    if (state.n == 1) {
      print('${state.source} -> ${state.target}');
      continue;
    }

    switch (state.stage) {
      case 0:
        // 第一次遇到这个状态，需要分解
        stack.add(state.copyWith(stage: 1));
        stack.add(HanoiState(
          n: state.n - 1,
          source: state.source,
          target: state.auxiliary,
          auxiliary: state.target,
          stage: 0,
        ));
        break;

      case 1:
        // 第一个递归完成，移动最大圆盘
        stack.add(state.copyWith(stage: 2));
        print('${state.source} -> ${state.target}');
        stack.add(HanoiState(
          n: state.n - 1,
          source: state.auxiliary,
          target: state.target,
          auxiliary: state.source,
          stage: 0,
        ));
        break;

      case 2:
        // 所有递归完成
        break;
    }
  }
}

---

五、算法优化

5.1 尾递归优化

// 标准递归（非尾递归）
void hanoi(int n, String source, String target, String auxiliary) {
  if (n == 1) {
    moves.add([source, target]);
    return;
  }
  hanoi(n - 1, source, auxiliary, target);
  moves.add([source, target]);
  hanoi(n - 1, auxiliary, target, source);
}

// 尾递归优化版本
void hanoiTail(int n, String source, String target, String auxiliary, List<List<String>> moves) {
  if (n == 1) {
    moves.add([source, target]);
    return;
  }

  // 使用累积参数
  _hanoiHelper(n, source, target, auxiliary, moves, 0);
}

void _hanoiHelper(int n, String source, String target, String auxiliary,
                   List<List<String>> moves, int level) {
  if (n == 1) {
    moves.add([source, target]);
    return;
  }

  // 处理n-1个圆盘到辅助塔
  _hanoiHelper(n - 1, source, auxiliary, target, moves, level + 1);

  // 移动最大圆盘
  moves.add([source, target]);

  // 处理n-1个圆盘从辅助塔到目标塔
  _hanoiHelper(n - 1, auxiliary, target, source, moves, level + 1);
}

5.2 记忆化优化

虽然标准汉诺塔不需要记忆化（每个子问题只计算一次），但如果要多次查询某些状态，可以使用记忆化：

class HanoiMemo {
  final Map<String, List<List<String>>> _cache = {};

  List<List<String>> solve(int n, String source, String target, String auxiliary) {
    final key = '$n-$source-$target-$auxiliary';

    if (_cache.containsKey(key)) {
      return _cache[key]!;
    }

    if (n == 1) {
      final result = [[source, target]];
      _cache[key] = result;
      return result;
    }

    final moves1 = solve(n - 1, source, auxiliary, target);
    final move2 = [source, target];
    final moves3 = solve(n - 1, auxiliary, target, source);

    final result = [
      ...moves1,
      move2,
      ...moves3,
    ];

    _cache[key] = result;
    return result;
  }
}

---

六、变种问题

6.1 双向汉诺塔

// 双向汉诺塔：两个玩家同时从两端移动
class BiDirectionalHanoi {
  final List<Disk> leftTower = [];
  final List<Disk> rightTower = [];
  final List<Disk> middleTower = [];

  void moveLeftDisk() {
    if (leftTower.isEmpty) return;

    final disk = leftTower.last;
    if (middleTower.isEmpty || disk.size < middleTower.last.size) {
      middleTower.add(leftTower.removeLast());
    }
  }

  void moveRightDisk() {
    if (rightTower.isEmpty) return;

    final disk = rightTower.last;
    if (middleTower.isEmpty || disk.size < middleTower.last.size) {
      middleTower.add(rightTower.removeLast());
    }
  }

  bool isLeftWin() => middleTower.length == leftTower.length + rightTower.length;
  bool isRightWin() => middleTower.length == leftTower.length + rightTower.length;
}

6.2 Reve’s Puzzle（四塔问题）

// 四塔汉诺塔（Reve's Puzzle）
int hanoi4(int n, String source, String target, String aux1, String aux2) {
  if (n == 0) return 0;
  if (n == 1) {
    print('$source -> $target');
    return 1;
  }

  // Frame-Stewart算法
  int minMoves = double.maxFinite.toInt();

  for (int k = 0; k < n; k++) {
    final moves1 = hanoi4(k, source, aux1, target, aux2);
    final moves2 = hanoi3(n - k, source, target, aux2);
    final moves3 = hanoi4(k, aux1, target, source, aux2);
    final totalMoves = moves1 + moves2 + moves3;

    if (totalMoves < minMoves) {
      minMoves = totalMoves;
    }
  }

  return minMoves;
}

int hanoi3(int n, String source, String target, String auxiliary) {
  if (n == 0) return 0;
  if (n == 1) {
    print('$source -> $target');
    return 1;
  }

  final moves1 = hanoi3(n - 1, source, auxiliary, target);
  final move2 = 1;
  print('$source -> $target');
  final moves3 = hanoi3(n - 1, auxiliary, target, source);

  return moves1 + move2 + moves3;
}

---

七、可视化算法

7.1 移动步骤可视化

class HanoiVisualizer {
  late List<Tower> towers;
  late List<List<String>> moves;
  late List<int> moveNumbers;  // 每步涉及的圆盘

  void initialize(int n) {
    towers = [
      Tower('A'),
      Tower('B'),
      Tower('C'),
    ];

    // 在源塔上创建圆盘
    for (int i = n; i >= 1; i--) {
      towers[0].push(Disk(size: i, color: Colors.blue));
    }

    moves = [];
    moveNumbers = [];
    _hanoi(n, 0, 2, 1);
  }

  void _hanoi(int n, int source, int target, int auxiliary) {
    if (n == 1) {
      moves.add([towers[source].name, towers[target].name]);
      moveNumbers.add(n);
      return;
    }

    _hanoi(n - 1, source, auxiliary, target);
    moves.add([towers[source].name, towers[target].name]);
    moveNumbers.add(n);
    _hanoi(n - 1, auxiliary, target, source);
  }

  // 获取指定步骤的状态
  List<Tower> getStateAtStep(int step) {
    final result = List.generate(3, (i) => Tower(towers[i].name));

    // 复制初始状态
    for (final disk in towers[0].disks) {
      result[0].push(Disk(size: disk.size, color: disk.color));
    }

    // 执行前step步
    for (int i = 0; i < step && i < moves.length; i++) {
      final fromName = moves[i][0];
      final toName = moves[i][1];

      final fromIndex = result.indexWhere((t) => t.name == fromName);
      final toIndex = result.indexWhere((t) => t.name == toName);

      if (fromIndex >= 0 && toIndex >= 0) {
        final disk = result[fromIndex].pop();
        result[toIndex].push(disk);
      }
    }

    return result;
  }

  // 获取圆盘移动路径
  List<Point> getDiskPath(int diskSize, int fromStep, int toStep) {
    final path = <Point>[];

    for (int step = fromStep; step <= toStep && step < moves.length; step++) {
      if (moveNumbers[step] == diskSize) {
        // 计算圆盘在这一步的位置
        final state = getStateAtStep(step);
        for (int i = 0; i < state.length; i++) {
          for (int j = 0; j < state[i].disks.length; j++) {
            if (state[i].disks[j].size == diskSize) {
              path.add(Point(i, j));
              break;
            }
          }
        }
      }
    }

    return path;
  }
}

---

八、总结

本文深入讲解了汉诺塔问题的算法原理，主要内容包括：

1. 数学原理：最少步数证明、数列分析
2. 递归分析：递归树、递归方程、栈空间
3. 动画执行：自动求解、状态管理、定时器控制
4. 迭代解法：二进制表示、栈模拟
5. 算法优化：尾递归、记忆化
6. 变种问题：双向汉诺塔、四塔问题
7. 可视化：步骤可视化、路径追踪

通过本文的学习，读者可以：

• 理解递归算法的本质和实现方式
• 掌握栈数据结构在汉诺塔中的应用
• 学会使用Timer实现动画效果
• 了解如何将递归算法转化为可视化界面
• 掌握Flutter状态管理的最佳实践

核心代码实现：

• 递归算法：_hanoi() 方法生成移动步骤
• 动画执行：_executeMoves() 方法逐步执行动画
• 状态管理：使用 setState() 更新UI
• 交互设计：点击选择塔进行移动

掌握这些知识可以让你深入理解递归算法的本质，并将其应用到更复杂的问题中。

---

欢迎加入开源鸿蒙跨平台社区: 开源鸿蒙跨平台开发者社区