Flutter for OpenHarmony 实战:数独算法与求解器深度解析
摘要 本文深入解析数独游戏的算法实现,重点探讨回溯求解算法的优化策略与约束传播技术。内容包括基础回溯算法实现及其时间复杂度分析(O(9^m)),以及最小剩余值(MRV)和前向检查等优化方法。同时介绍了单元传播(Naked Single)和隐性单数(Hidden Single)等约束传播技术,展示了如何将人类逻辑转化为高效算法。通过优化候选数计算和约束检查,显著提升数独求解性能,为开发者实现高性能数
·
欢迎加入开源鸿蒙跨平台社区:开源鸿蒙跨平台开发者社区
Flutter for OpenHarmony 实战:数独算法与求解器深度解析
文章目录
摘要
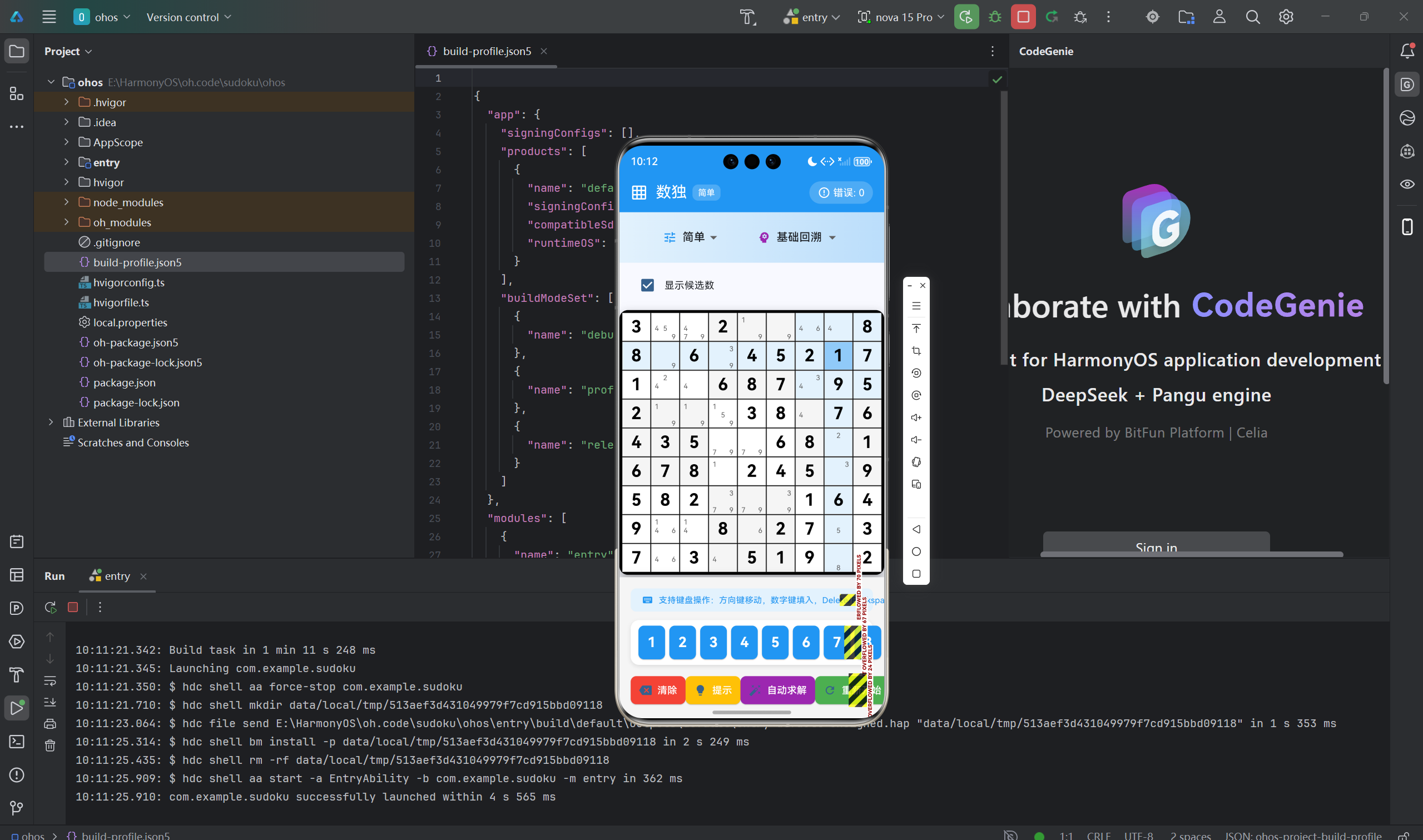
数独游戏看似简单,但其背后蕴含了丰富的算法设计与优化技巧。本文深入探讨数独的核心算法实现,包括回溯求解算法的优化、约束传播技术、人类求解策略、唯一解验证等高级主题。通过本文学习,读者将掌握约束满足问题(CSP)的解决方法,了解如何将人类逻辑转化为算法实现,提升游戏性能和用户体验。
一、回溯算法深度解析
1.1 算法原理
回溯算法是一种通过穷举所有可能解来寻找问题解的方法。对于数独来说:
- 找到第一个空白格
- 尝试填入1-9
- 检查是否违反约束
- 递归处理下一个空白格
- 如果无解则回溯
1.2 基础回溯实现
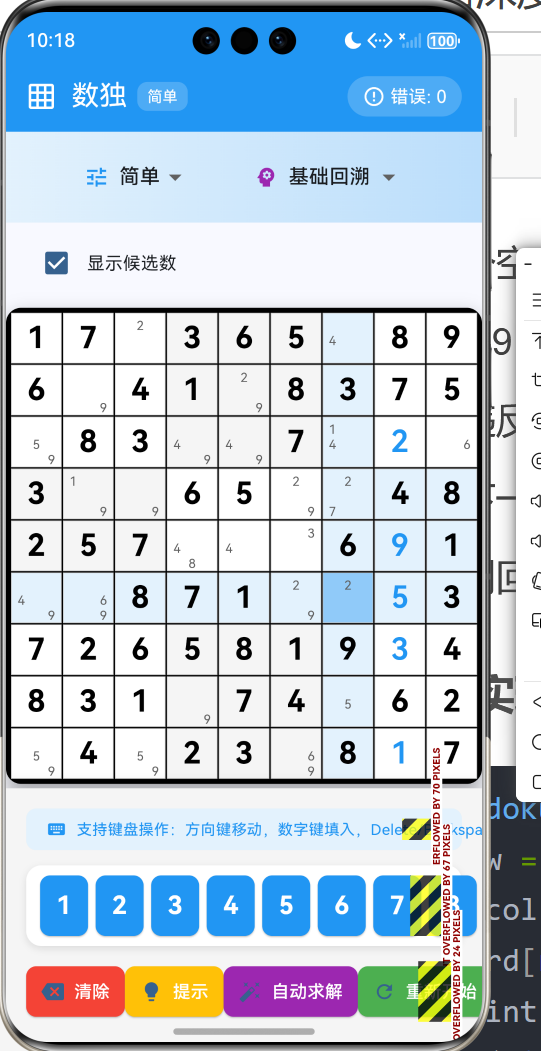
bool _solveSudoku(List<List<int>> board) {
for (int row = 0; row < 9; row++) {
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0) {
for (int num = 1; num <= 9; num++) {
if (_isValid(board, row, col, num)) {
board[row][col] = num;
if (_solveSudoku(board)) {
return true;
}
board[row][col] = 0; // 回溯
}
}
return false;
}
}
}
return true;
}
时间复杂度:O(9^m),m为空白格数量
空间复杂度:O(m) - 递归栈深度
1.3 最小剩余值(MRV)优化
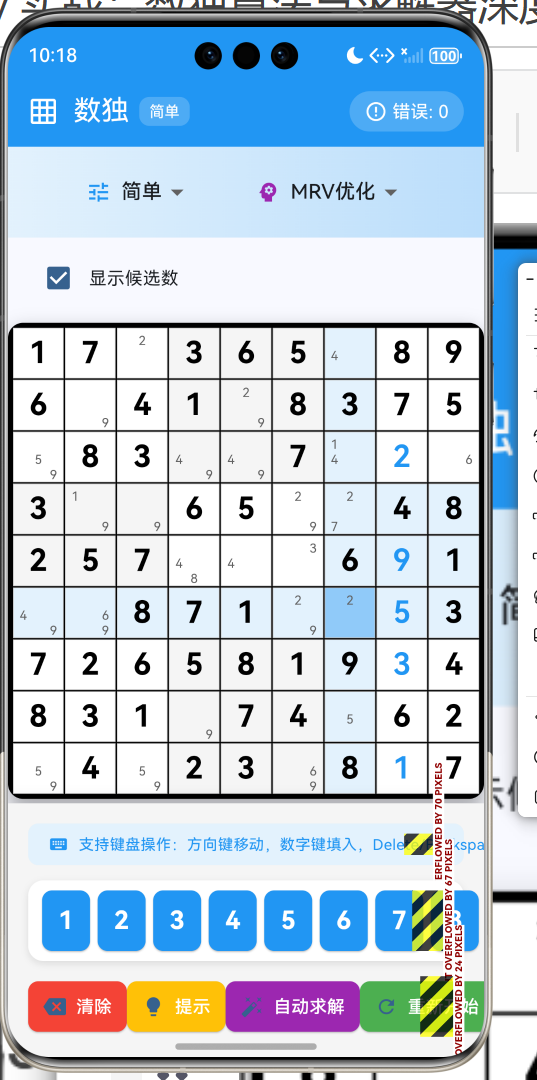
优先选择候选数最少的格子:
bool _solveSudokuMRV(List<List<int>> board) {
// 找到候选数最少的空白格
final minCell = _findMinimumRemainingValues(board);
if (minCell == null) {
return true; // 已填满
}
final row = minCell['row']!;
final col = minCell['col']!;
final candidates = _getCandidates(board, row, col);
for (final num in candidates) {
board[row][col] = num;
if (_solveSudokuMRV(board)) {
return true;
}
board[row][col] = 0;
}
return false;
}
Map<String, int>? _findMinimumRemainingValues(List<List<int>> board) {
int minCount = 10;
Map<String, int>? minCell;
for (int row = 0; row < 9; row++) {
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0) {
final candidates = _getCandidates(board, row, col);
if (candidates.length < minCount) {
minCount = candidates.length;
minCell = {'row': row, 'col': col};
}
}
}
}
return minCell;
}
List<int> _getCandidates(List<List<int>> board, int row, int col) {
final used = <int>{};
// 检查行
for (int c = 0; c < 9; c++) {
if (board[row][c] != 0) used.add(board[row][c]);
}
// 检查列
for (int r = 0; r < 9; r++) {
if (board[r][col] != 0) used.add(board[r][col]);
}
// 检查3x3宫格
final boxRow = (row ~/ 3) * 3;
final boxCol = (col ~/ 3) * 3;
for (int r = 0; r < 3; r++) {
for (int c = 0; c < 3; c++) {
if (board[boxRow + r][boxCol + c] != 0) {
used.add(board[boxRow + r][boxCol + c]);
}
}
}
// 返回未使用的数字
final candidates = <int>[];
for (int num = 1; num <= 9; num++) {
if (!used.contains(num)) {
candidates.add(num);
}
}
return candidates;
}
1.4 前向检查优化
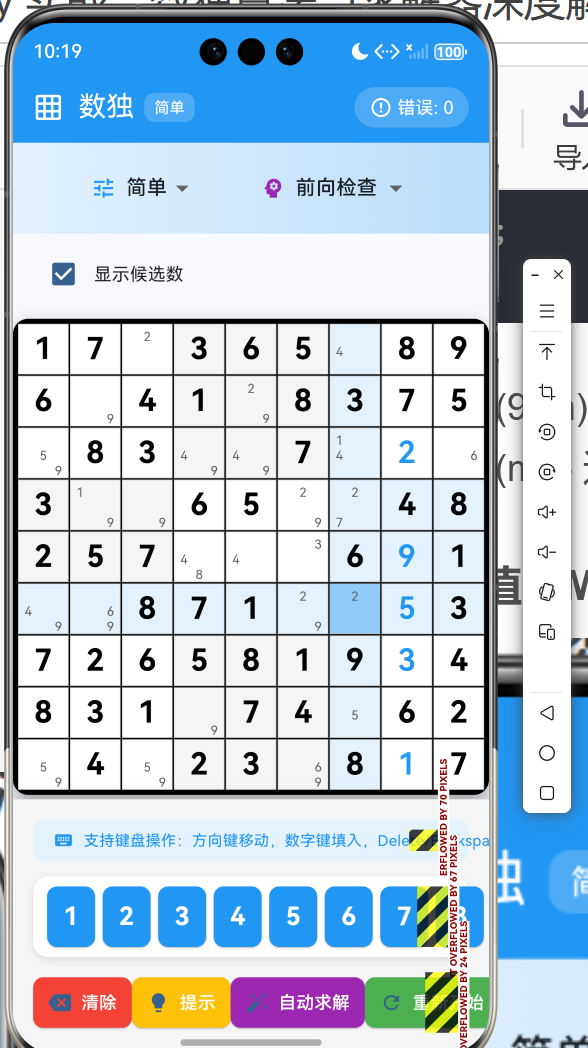
在填入数字后,立即检查是否会导致其他格子无解:
bool _solveSudokuForwardChecking(List<List<int>> board) {
final emptyCells = _getEmptyCells(board);
if (emptyCells.isEmpty) return true;
// 按候选数排序
emptyCells.sort((a, b) {
final candidatesA = _getCandidates(board, a['row']!, a['col']!);
final candidatesB = _getCandidates(board, b['row']!, b['col']!);
return candidatesA.length.compareTo(candidatesB.length);
});
final cell = emptyCells.first;
final row = cell['row']!;
final col = cell['col']!;
for (final num in _getCandidates(board, row, col)) {
board[row][col] = num;
// 前向检查:确保所有空白格仍有至少一个候选数
if (_forwardCheck(board)) {
if (_solveSudokuForwardChecking(board)) {
return true;
}
}
board[row][col] = 0;
}
return false;
}
bool _forwardCheck(List<List<int>> board) {
for (int row = 0; row < 9; row++) {
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0) {
if (_getCandidates(board, row, col).isEmpty) {
return false;
}
}
}
}
return true;
}
List<Map<String, int>> _getEmptyCells(List<List<int>> board) {
final cells = <Map<String, int>>[];
for (int row = 0; row < 9; row++) {
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0) {
cells.add({'row': row, 'col': col});
}
}
}
return cells;
}
二、约束传播技术
2.1 单元传播(Naked Single)
如果一个格子只有一个可能的候选数,直接填入:
bool _applyNakedSingles(List<List<int>> board) {
bool changed = false;
for (int row = 0; row < 9; row++) {
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0) {
final candidates = _getCandidates(board, row, col);
if (candidates.length == 1) {
board[row][col] = candidates.first;
changed = true;
}
}
}
}
return changed;
}
2.2 隐性单数(Hidden Single)
如果一个数字在某行/列/宫格中只能填入一个位置:
bool _applyHiddenSingles(List<List<int>> board) {
bool changed = false;
// 检查每一行
for (int row = 0; row < 9; row++) {
changed |= _applyHiddenSinglesInRow(board, row);
}
// 检查每一列
for (int col = 0; col < 9; col++) {
changed |= _applyHiddenSinglesInCol(board, col);
}
// 检查每个3x3宫格
for (int boxRow = 0; boxRow < 3; boxRow++) {
for (int boxCol = 0; boxCol < 3; boxCol++) {
changed |= _applyHiddenSinglesInBox(board, boxRow, boxCol);
}
}
return changed;
}
bool _applyHiddenSinglesInRow(List<List<int>> board, int row) {
bool changed = false;
for (int num = 1; num <= 9; num++) {
final positions = <int>[];
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0 && _canPlace(board, row, col, num)) {
positions.add(col);
}
}
if (positions.length == 1) {
board[row][positions.first] = num;
changed = true;
}
}
return changed;
}
bool _applyHiddenSinglesInCol(List<List<int>> board, int col) {
bool changed = false;
for (int num = 1; num <= 9; num++) {
final positions = <int>[];
for (int row = 0; row < 9; row++) {
if (board[row][col] == 0 && _canPlace(board, row, col, num)) {
positions.add(row);
}
}
if (positions.length == 1) {
board[positions.first][col] = num;
changed = true;
}
}
return changed;
}
bool _applyHiddenSinglesInBox(List<List<int>> board, int boxRow, int boxCol) {
bool changed = false;
for (int num = 1; num <= 9; num++) {
final positions = <Map<String, int>>[];
for (int r = 0; r < 3; r++) {
for (int c = 0; c < 3; c++) {
final row = boxRow * 3 + r;
final col = boxCol * 3 + c;
if (board[row][col] == 0 && _canPlace(board, row, col, num)) {
positions.add({'row': row, 'col': col});
}
}
}
if (positions.length == 1) {
final pos = positions.first;
board[pos['row']!][pos['col']!] = num;
changed = true;
}
}
return changed;
}
bool _canPlace(List<List<int>> board, int row, int col, int num) {
return _isValid(board, row, col, num);
}
三、人类求解策略
3.1 唯一候选数
最基础的策略,直接填入只有一个候选数的格子:
void _hintOnlyCandidate(List<List<int>> board, int row, int col) {
if (board[row][col] != 0) return;
final candidates = _getCandidates(board, row, col);
if (candidates.length == 1) {
board[row][col] = candidates.first;
}
}
3.2 唯一位置
在某个行/列/宫格中,某个数字只能填在一个位置:
void _hintUniquePosition(List<List<int>> board, int row, int col) {
if (board[row][col] != 0) return;
final candidates = _getCandidates(board, row, col);
for (final num in candidates) {
// 检查行中其他位置是否都不能填num
bool uniqueInRow = true;
for (int c = 0; c < 9; c++) {
if (c != col && board[row][c] == 0 && _isValid(board, row, c, num)) {
uniqueInRow = false;
break;
}
}
if (uniqueInRow) {
board[row][col] = num;
return;
}
// 检查列中其他位置是否都不能填num
bool uniqueInCol = true;
for (int r = 0; r < 9; r++) {
if (r != row && board[r][col] == 0 && _isValid(board, r, col, num)) {
uniqueInCol = false;
break;
}
}
if (uniqueInCol) {
board[row][col] = num;
return;
}
// 检查3x3宫格中其他位置是否都不能填num
final boxRow = (row ~/ 3) * 3;
final boxCol = (col ~/ 3) * 3;
bool uniqueInBox = true;
for (int r = 0; r < 3; r++) {
for (int c = 0; c < 3; c++) {
final curR = boxRow + r;
final curC = boxCol + c;
if ((curR != row || curC != col) &&
board[curR][curC] == 0 &&
_isValid(board, curR, curC, num)) {
uniqueInBox = false;
break;
}
}
}
if (uniqueInBox) {
board[row][col] = num;
return;
}
}
}
3.3 排除法(Naked Pairs/Triples)
如果在某行/列/宫格中,两个格子只有相同的两个候选数,则这两个数可以从该区域其他格子中排除:
bool _applyNakedPairs(List<List<int>> board) {
bool changed = false;
// 检查每一行
for (int row = 0; row < 9; row++) {
changed |= _applyNakedPairsInRow(board, row);
}
// 检查每一列
for (int col = 0; col < 9; col++) {
changed |= _applyNakedPairsInCol(board, col);
}
// 检查每个3x3宫格
for (int boxRow = 0; boxRow < 3; boxRow++) {
for (int boxCol = 0; boxCol < 3; boxCol++) {
changed |= _applyNakedPairsInBox(board, boxRow, boxCol);
}
}
return changed;
}
bool _applyNakedPairsInRow(List<List<int>> board, int row) {
final emptyCols = <int>[];
final candidatesMap = <int, List<int>>{};
// 收集空白格及其候选数
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0) {
final candidates = _getCandidates(board, row, col);
if (candidates.length == 2) {
emptyCols.add(col);
candidatesMap[col] = candidates;
}
}
}
// 查找naked pairs
for (int i = 0; i < emptyCols.length; i++) {
for (int j = i + 1; j < emptyCols.length; j++) {
final col1 = emptyCols[i];
final col2 = emptyCols[j];
final cand1 = candidatesMap[col1]!;
final cand2 = candidatesMap[col2]!;
if (cand1[0] == cand2[0] && cand1[1] == cand2[1]) {
// 找到naked pair,从其他格子排除这两个候选数
for (int col = 0; col < 9; col++) {
if (col != col1 && col != col2 && board[row][col] == 0) {
final oldCandidates = _getCandidates(board, row, col);
final newCandidates = oldCandidates.where((n) =>
!cand1.contains(n)
).toList();
if (newCandidates.length == 1) {
board[row][col] = newCandidates.first;
return true;
}
}
}
}
}
}
return false;
}
四、完整求解器实现
4.1 结合约束传播和回溯
class SudokuSolver {
bool solve(List<List<int>> board) {
// 先应用约束传播
while (_applyConstraints(board)) {
// 持续应用直到没有变化
}
// 检查是否已解决
if (_isComplete(board)) {
return true;
}
// 检查是否无效
if (_isInvalid(board)) {
return false;
}
// 使用回溯解决剩余部分
return _solveWithBacktracking(board);
}
bool _applyConstraints(List<List<int>> board) {
bool changed = false;
// 应用各种约束传播技术
changed |= _applyNakedSingles(board);
changed |= _applyHiddenSingles(board);
changed |= _applyNakedPairs(board);
return changed;
}
bool _isComplete(List<List<int>> board) {
for (int row = 0; row < 9; row++) {
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0) return false;
}
}
return true;
}
bool _isInvalid(List<List<int>> board) {
for (int row = 0; row < 9; row++) {
for (int col = 0; col < 9; col++) {
if (board[row][col] == 0) {
if (_getCandidates(board, row, col).isEmpty) {
return true;
}
}
}
}
return false;
}
bool _solveWithBacktracking(List<List<int>> board) {
final minCell = _findMinimumRemainingValues(board);
if (minCell == null) {
return true;
}
final row = minCell['row']!;
final col = minCell['col']!;
final candidates = _getCandidates(board, row, col);
for (final num in candidates) {
final boardCopy = _copyBoard(board);
boardCopy[row][col] = num;
if (solve(boardCopy)) {
// 复制解回原board
for (int r = 0; r < 9; r++) {
for (int c = 0; c < 9; c++) {
board[r][c] = boardCopy[r][c];
}
}
return true;
}
}
return false;
}
List<List<int>> _copyBoard(List<List<int>> board) {
return List.generate(9, (r) =>
List.generate(9, (c) => board[r][c])
);
}
}
五、难度评估算法
5.1 基于求解步骤的难度评估
class SudokuDifficultyEvaluator {
DifficultyRating evaluate(List<List<int>> board) {
final solver = SudokuSolver();
final steps = solver.solveWithSteps(board);
final techniqueCount = <String, int>{};
for (final step in steps) {
techniqueCount[step.technique] =
(techniqueCount[step.technique] ?? 0) + 1;
}
// 根据使用的技术评估难度
if (techniqueCount.containsKey('nakedSingle') &&
techniqueCount.length == 1) {
return DifficultyRating.easy;
} else if (techniqueCount.containsKey('hiddenSingle') &&
!techniqueCount.containsKey('nakedPairs')) {
return DifficultyRating.medium;
} else if (techniqueCount.containsKey('nakedPairs')) {
return DifficultyRating.hard;
} else {
return DifficultyRating.expert;
}
}
}
class SolutionStep {
final String technique;
final int row;
final int col;
final int value;
SolutionStep({
required this.technique,
required this.row,
required this.col,
required this.value,
});
}
enum DifficultyRating {
easy,
medium,
hard,
expert,
}
六、总结
本文深入探讨了数独算法的核心技术:
- 回溯算法优化:MRV、前向检查
- 约束传播:单元传播、隐性单数
- 人类求解策略:唯一候选数、唯一位置、排除法
- 完整求解器:结合多种技术的高效求解
- 难度评估:基于求解步骤的难度分级
这些算法技术不仅适用于数独游戏,也可以应用到其他约束满足问题(CSP)中。
欢迎加入开源鸿蒙跨平台社区: 开源鸿蒙跨平台开发者社区
更多推荐
 已为社区贡献9条内容
已为社区贡献9条内容






所有评论(0)