P3375 【模板】KMP

题目描述

给出两个字符串 $s_1$ 和 $s_2$，若 $s_1$ 的区间 $[l,r]$ 子串与 $s_2$ 完全相同，则称 $s_2$ 在 $s_1$ 中出现了，其出现位置为 $l$。
现在请你求出 $s_2$ 在 $s_1$ 中所有出现的位置。

定义一个字符串 $s$ 的 border 为 $s$ 的一个非 $s$ 本身的子串 $t$，满足 $t$ 既是 $s$ 的前缀，又是 $s$ 的后缀。
对于 $s_2$，你还需要求出对于其每个前缀 $s^{\prime }$ 的最长 border $t^{\prime }$ 的长度。

输入格式

第一行为一个字符串，即为 $s_1$。
第二行为一个字符串，即为 $s_2$。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 $s_2$ 在 $s_1$ 中出现的位置。
最后一行输出 $|s_2|$ 个整数，第 $i$ 个整数表示 $s_2$ 的长度为 $i$ 的前缀的最长 border 长度。

输入输出样例 #1

输入 #1

ABABABC
ABA

输出 #1

1
3
0 0 1 

说明/提示

样例 1 解释

。

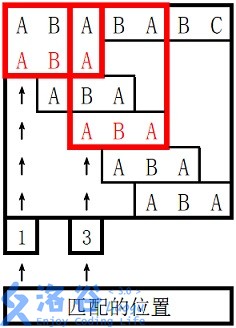对于 $s_2$ 长度为 $3$ 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 $1$。

数据规模与约定

本题采用多测试点捆绑测试，共有 4 个子任务。

• Subtask 0（30 points）：$|s_1|\le 15$，$|s_2|\le 5$。
• Subtask 1（40 points）：$|s_1|\le 10^4$，$|s_2|\le 10^2$。
• Subtask 2（30 points）：无特殊约定。
• Subtask 3（0 points）：Hack。

对于全部的测试点，保证 $1\le |s_1|,|s_2|\le 10^6$，$s_1,s_2$ 中均只含大写英文字母。

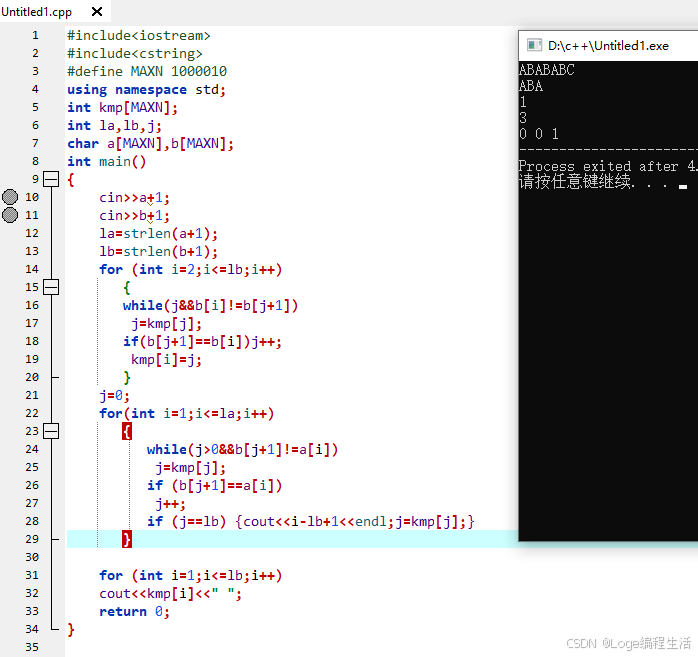
C++实现

#include<iostream>
#include<cstring>
#define MAXN 1000010
using namespace std;
int kmp[MAXN];
int la,lb,j; 
char a[MAXN],b[MAXN];
int main()
{
    cin>>a+1;
    cin>>b+1;
    la=strlen(a+1);
    lb=strlen(b+1);
    for (int i=2;i<=lb;i++)
	   {     
	   while(j&&b[i]!=b[j+1])
        j=kmp[j];    
       if(b[j+1]==b[i])j++;    
        kmp[i]=j;
       }
    j=0;
    for(int i=1;i<=la;i++)
	   {
          while(j>0&&b[j+1]!=a[i])
           j=kmp[j];
          if (b[j+1]==a[i]) 
           j++;
          if (j==lb) {cout<<i-lb+1<<endl;j=kmp[j];}
       }

    for (int i=1;i<=lb;i++)
    cout<<kmp[i]<<" ";
    return 0;
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容