数据结构：kmp算法，Trie树，以及并查集的干货详解---小白也能看懂

kmp算法，Trie，并查集的详解及其模板

没死的脚皮

1479人浏览 · 2026-01-19 21:49:10

没死的脚皮 · 2026-01-19 21:49:10 发布

🎬 博主名称：个人主页

🔥 个人专栏: 《算法通关》，《Java讲解》

⛺️心简单，世界就简单

序言

昨晚数据结构写了一半，做图太累了，文章写的比较慢，这篇应该就是第二篇，后面还有一篇，太困了，真不行了

今天讲一下 kmp算法，Trie，并查集

KMP算法

这里说一下kmp的大致情况

用于处理字符串匹配问题，他也是十分的抽象给一个S[]主串（比较长的那个），P[]为模板串，kmp我们一般用下标1来开始遍历

接下来我们需要去思考的是

1，暴力去怎么做

2，怎么去优化

下面是暴力的模板代码

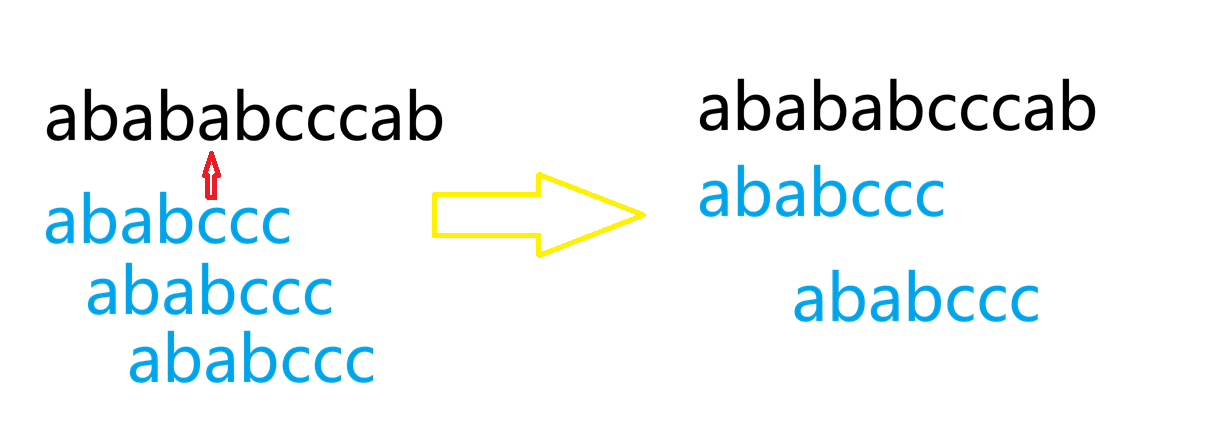
大概意思就是，每当我们匹配到不一样的部位，我们的P就要从头开始再跟刚刚s的起点+1位置重新匹配，这样就会造成串的长度很长时候，就会超时，所以我们就要从这个过程中找性质了

	 for(int i = 1; i <= m; i ++){//枚举当前的起点 
	 	bool flag = true;// 成功的状态 
	 	for(int j = 1; j <= n; j++){
		 	if(S[i+j-1] != P[j]){
			 	flag = false;
			 	break;
			 }
		 }
	 }

原理

看这个第一个是暴力，我们需要每次遇到不一样的字符，就让P从头开始，去匹配 S 串，这样我们其实可以发现 P 串他本身就会有一些相同的前缀后缀，然后当我们遇到不相同的字符，我们没必要再一个一个匹配，我们可以直接跳到一定位置接着继续匹配，这就是我们的原理

现在我们就要去思考，我们怎样找到，当一个位置匹配失败时，我们需要让这个串最多移动多少，这就是我们常常听说的next数组的用处了

next数组

next[ i ] 的含义就是以 i 为终点的这个后缀和从1开始的这个前缀相等，且这个长度最长

比如， next[ i ] = j,意思就是，p[ 1.....j] = p[ i - j + 1........i]

next数组咱咋求，我们先假设 i-1 位置（包括i-1这个位置）之前的最长的前缀和后缀的长度为 j ,如果此时 i 位置和 j + 1位置相等，那我们就在此基础上先 j ++,然后让ne[ i ] = j，如果就是位置不相等嘞，那我们就利用next[ j ]找到这个相等的前缀，然后继续匹配，也就是 j = ne[ j ]
好了大致就是这样，你一定要先知道next数组是干啥

for(int i = 1, j = 0;i <=m; i++ ){
		while(j && S[i] != P[j + 1]) j = ne[j];
		if(S[i] == P[j + 1]) j ++;
		if(j == n){
			//匹配成功
			printf("%d ", i - n);//减n是因为，字符串的位置是从0开始 
		    j = ne[j];//成功后可能后面还有能匹配的，继续操作 
		}
	}

	for(int i = 2, j = 0; i <= n;i ++){
		while(j && P[i] != P[j + 1]) j = ne[j];
		if(P[i] == P[j + 1]) j ++; 
		ne[i] = j;
	}

匹配过程

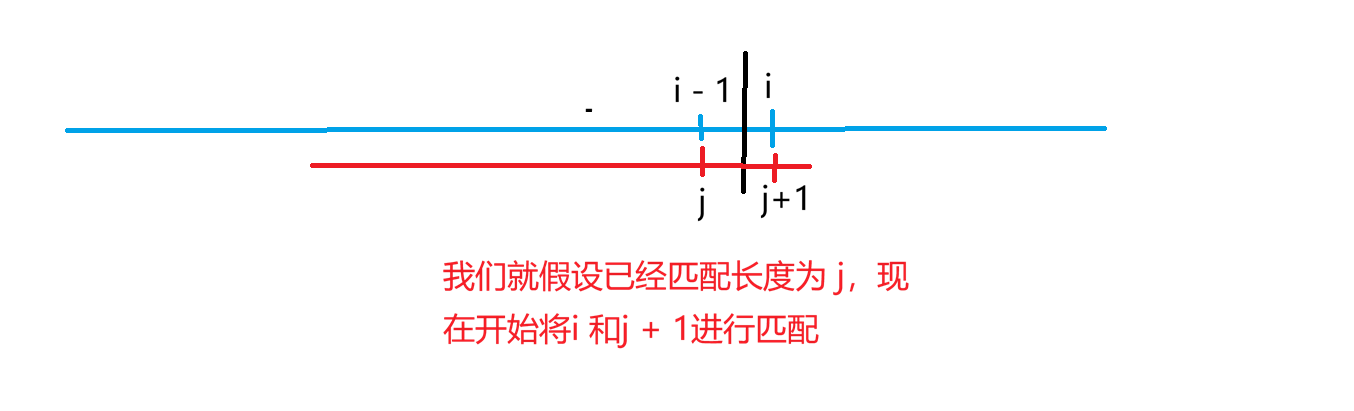
我们先明确指针，大概就是上面这个图，我们每次是要看j + 1 和 i位置是否相同，不同就让j退回到ne[ j ]位置，然后再看j + 1位置和 i 是否相同，如果相同我们就让j ++，然后让ne[ i ] 等于j

代码其实和构造next数组几乎一样

for(int i = 1, j = 0;i <=m; i++ ){
		while(j && S[i] != P[j + 1]) j = ne[j];
		if(S[i] == P[j + 1]) j ++;
		if(j == n){
			//匹配成功
			printf("%d ", i - n);//减n是因为，字符串的位置是从0开始 
		    j = ne[j];//成功后可能后面还有能匹配的，继续操作 
		}
	}

合起来就是这个，下面是题目模板

#include<iostream>

using namespace std;

const int N = 1e4 + 10;
const int M = 1e5 +10;
char S[M], P[N], ne[N], n, m;
int main(){
	cin >> n >> (P + 1) >> m >> (S + 1);
	
	//求next过程
	
	for(int i = 2, j = 0; i <= n;i ++){
		while(j && P[i] != P[j + 1]) j = ne[j];
		if(P[i] == P[j + 1]) j ++; 
		ne[i] = j;
	}
	 
	for(int i = 1, j = 0;i <=m; i++ ){
		while(j && S[i] != P[j + 1]) j = ne[j];
		if(S[i] == P[j + 1]) j ++;
		if(j == n){
			//匹配成功
			printf("%d ", i - n);//减n是因为，字符串的位置是从0开始 
		    j = ne[j];//成功后可能后面还有能匹配的，继续操作 
		}
	}
}

Trie树

用来快速的存储和查找字符串集合的数据结构

这个很简单我们来拿给题举例子

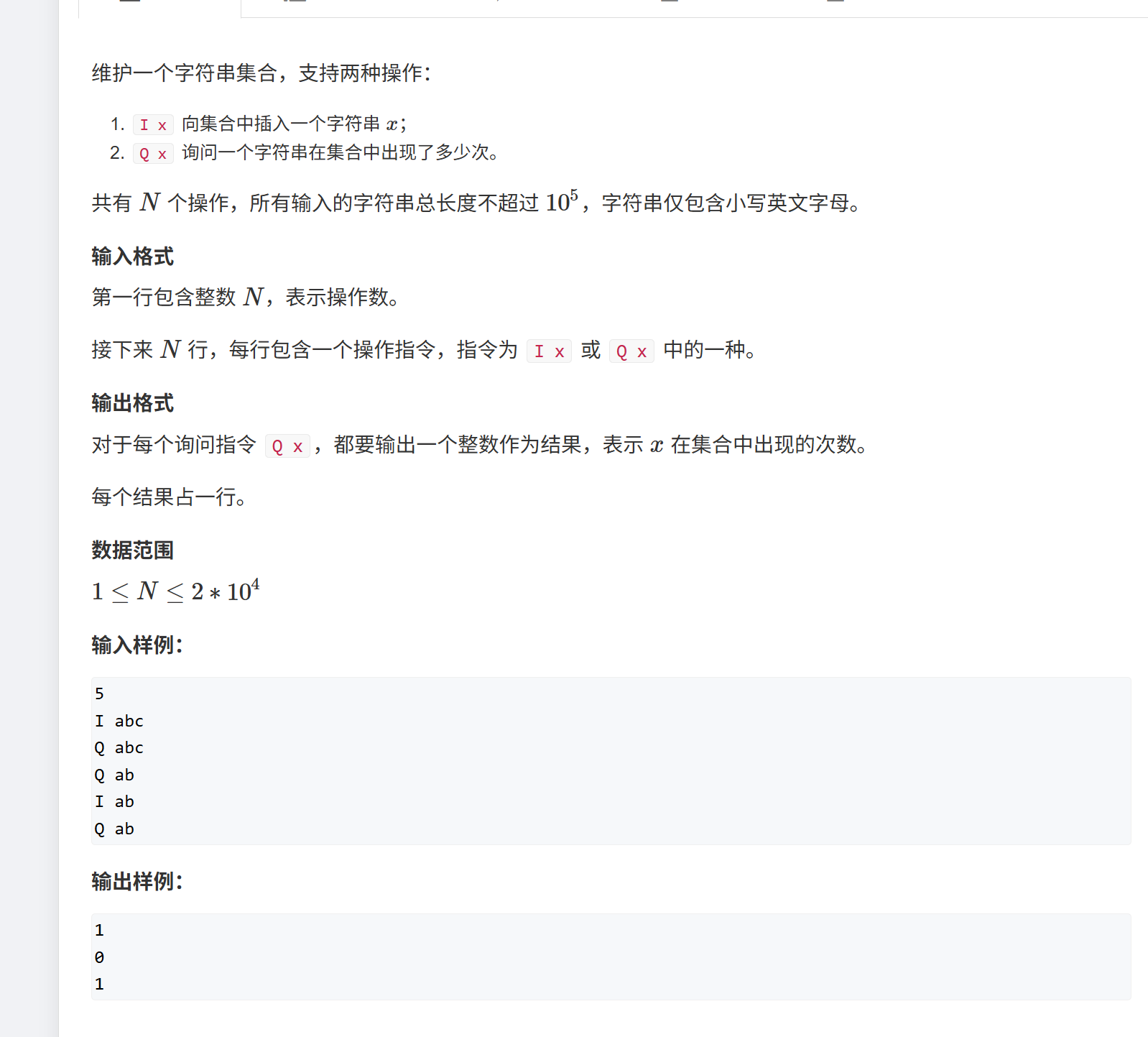
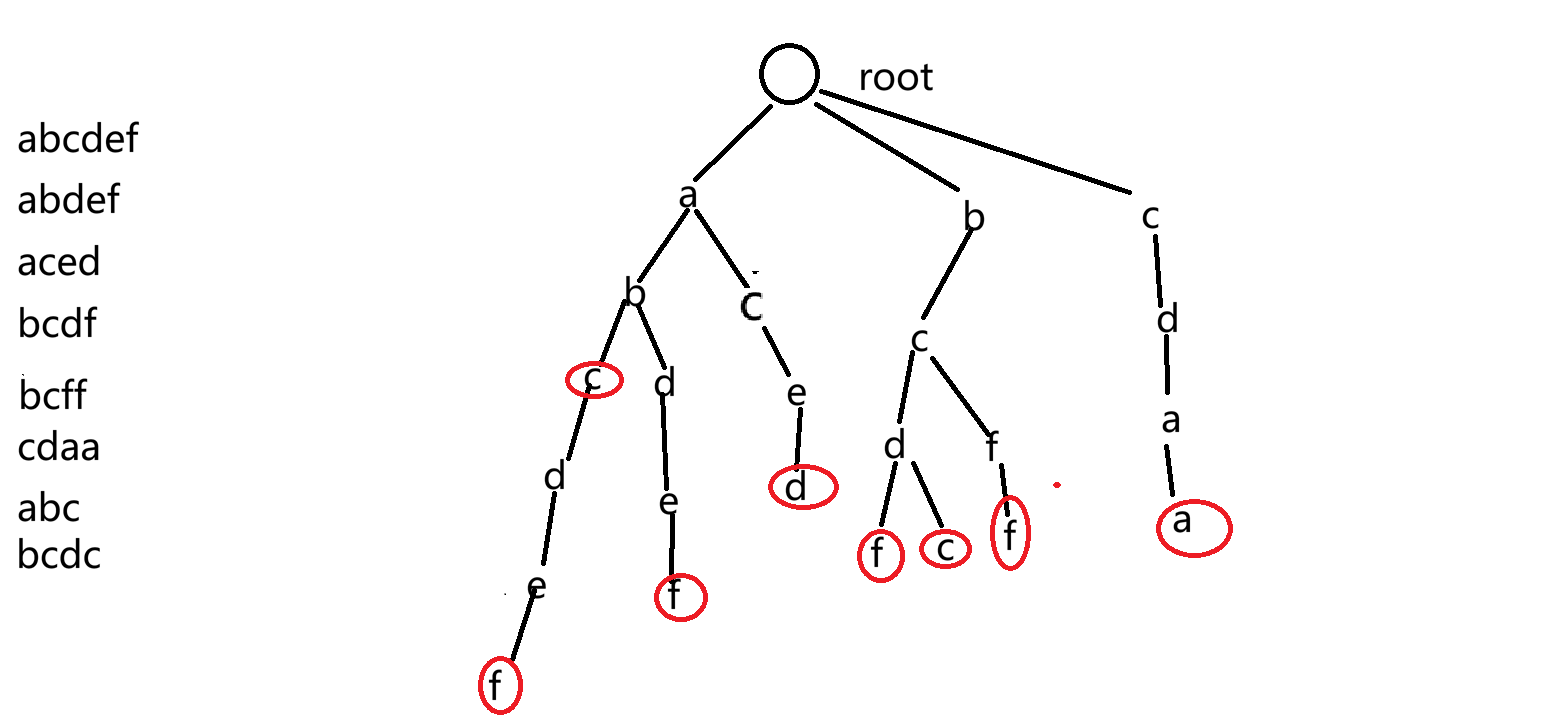
现在给了左侧这么多单词，我们来存进树里，我们从根节点开始，将每个单词的字母一一存进去，另外我们给最后一个字母做上标记，防止少走某些点

#include<iostream>

using namespace std;

const int N = 1e5 + 10;

char str[N];
int son[N][26], cnt[N], idx;//下标是0的带你，既是根节点又是 空节点 
//cnt是以当前这个点结尾的单词有多少个

//插入操作
void insert(char str[]){
	int p = 0;//从根节点开始，从0开始遍历 
	for(int i = 0; str[i]; i ++){
		int u = str[i] - 'a';
		//如果p这个节点不存在u这个儿子，就创建一个 
		if(!son[p][u]) son[p][u] = ++idx;
		p = son[p][u]; 
	}
	cnt[p]++;
} 

//查询操作
int query(char str[]){
	int p = 0;
	for(int i = 0; str[i]; i ++){
		int u = str[i] - 'a';
		if(!son[p][u]) return 0;
		p = son[p][u];
	}
	return cnt[p];
} 
int main(){
	int n;
	scanf("%d", &n);
	while(n --){
		char op[2];
		scanf("%s%s", op, str);
		if(op[0]=='I') insert(str);
		else printf("%d\n", query(str));
	}
}

并查集

我们先知道并查集是干啥的

1，他是将两个集合合并

2，询问两个元素是否在一个集合中

基本原理：每个集合用一颗树来表示，树根的编号就是整个集合的编号，每个节点存储他的父节点，p[ x ]表示父节点

问题 1：如何判断树根：if（p[ x ] == x)

问题2 ：如何求x的集合编号：while( p[ x ] !=x) x = p[ x ];

问题3：如何合并两个集合：假设p[ x ]是x的集合编号，p[ y ] 是y的集合编号，直接让这两个其中一个插到集合根-------p[ find(x) ] = p[ u ]

优化：路径压缩

下面展示一下并查集模板

#include<iostream>

using namespace std;

const int N = 1e5 + 10;
int p[N], n, m;

int find(int x){
	//返回下的祖宗节点，路径压缩优化
	if(p[x] != x) p[x] = find(p[x]);
	return p[x]; 
}

int main(){
	cin>>n>>m;
	//最开始自己就是根 
	for(int i = 1; i <= n; i++) p[i] = i;
	
	while(m --){
		char op[2];
		int a, b;
		scanf("%s%d%d", op, &a, &b);
		
		if(op[0] == 'M') p[find(a)] = find(b);
		//合并操作让a的祖宗节点的父亲等于b的祖宗 
		else{
			//判断两个节点是不是在一个集合
			if(find(a)==find(b)) puts("Yes");
			else{
				puts("No")
			} 
		} 
	}
}

如果说我们要求出每一个集合的有多少个点呢

这时候我们添加一个size数组就行了，如果合并就让 sizes[find(b)] += sizes[find(a)];

如果两个点在一个集合就 continue

#include<iostream>

using namespace std;

const int N = 1e5 + 10;
int p[N], n, m, sizes[N];

int find(int x){
	//返回下的祖宗节点，路径压缩优化
	if(p[x] != x) p[x] = find(p[x]);
	return p[x]; 
}

int main(){
	cin>>n>>m;
	//最开始自己就是根 
	for(int i = 1; i <= n; i++) p[i] = i, sizes[i] = 1;
	
	while(m --){
		char op[5];
		int a, b;
		scanf("%s", op);
		
		if(op[0] == 'C') {
		scanf("%d%d", &a, &b);
		if(find(a) == find(b)) continue;
		sizes[find(b)] += sizes[find(a)];
		p[find(a)] = find(b);	
		}
		//合并操作让a的祖宗节点的父亲等于b的祖宗 
		else if(op[1] == '1'){
			scanf("%d%d", &a, &b);
			//判断两个节点是不是在一个集合
			if(find(a)==find(b)) puts("Yes");
			else{
				puts("No");
			} 
		} 
		else {
			scanf("%d", &a);
			printf("%d\n", sizes[find(a)]);
		}
	}
	
}