前言

在几何审美的历史长河中，曼陀罗（Mandala）与万花筒（Kaleidoscope）始终代表着秩序与繁复的平衡点。这种基于中心对称的视觉语言，本质上是空间在极坐标系下的周期性映射。当我们将线性音频信号通过 极坐标变换（Polar Coordinates Transformation） 投射到镜像对称空间时，原本随时间流逝的波动信号将转化为环状缠绕的几何艺术。本文将深入探讨极坐标变换的数学机理，并展示如何在 Flutter 与鸿蒙 NEXT 系统中构建一套绚丽的动态曼陀罗系统。

---

目录

1. 数学建模：极坐标系下的空间映射
2. 模型架构：对称性算子与分片渲染
3. 核心实现：基于 Canvas 变换的镜像算法
4. 逻辑映射：音频能量对几何形变的驱动
5. 鸿蒙 NEXT 平台的高性能渲染进阶
6. 结语

---

一、 数学建模：极坐标系下的空间映射

传统的 UI 布局基于笛卡尔坐标系 $(x,y)$，而曼陀罗艺术的基石是极坐标系 $(r,\theta )$。

1.1 坐标转换公式

平面上任意一点从极坐标到笛卡尔坐标的映射关系为：

在万花筒动效中，我们将半径 $r$ 定义为音频能量与正弦波动的耦合函数：

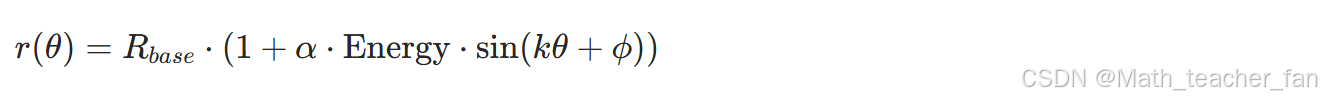
其中 $k$ 决定了花瓣的瓣数，$\varphi$ 随系统时钟偏移，产生动态流转的旋转感。

---

二、 模型架构：对称性算子与分片渲染

为了实现高效的对称绘制，我们不直接计算所有点的坐标，而是定义一个“基本分片（Base Slice）”，通过 Canvas 的旋转与缩放算子进行克隆。

---

三、 核心实现：基于 Canvas 变换的镜像算法

通过 canvas.rotate() 和 canvas.scale(1, -1)，我们可以轻松实现任意阶数的镜像对称。

3.1 分片迭代逻辑

for (int i = 0; i < segments; i++) {
  canvas.save();
  canvas.translate(center.dx, center.dy);
  canvas.rotate(i * angleStep + rotation * 2 * pi);
  
  // 绘制基础分片，i%2==0 用于产生镜像对称
  _drawSlice(canvas, size, i % 2 == 0);
  
  canvas.restore();
}

---

四、 逻辑映射：音频能量对几何形变的驱动

音频信号的脉冲被转化为分形边界的向外扩张力。

4.1 几何特性映射表

维度	音频特征	几何表现	视觉心理
半径 ®	总体音量	图形的扩张与收缩	呼吸感/生命力
扰动频率 (k)	高频能量	边缘的锯齿与分化程度	尖锐度/现代感
旋转速度	节奏快慢	镜像空间的扭转速率	眩晕感/迷幻美学
层叠数	频谱复杂度	几何图案的嵌套深度	秩序感/仪式感

---

五、 鸿蒙 NEXT 平台的高性能渲染进阶

在鸿蒙 NEXT 系统的架构下，面对这种复杂的几何变换，我们推荐以下优化方案：

1. 路径预构建 (Path Pre-caching)：利用 PathMetric 预先计算复杂的分片路径，避免在 paint 循环中频繁调用 cubicTo。
2. 离屏绘制 (Offscreen Canvas)：对于对称性高的静态部分，使用 PictureRecorder 录制分片，在主 Canvas 仅执行旋转位图指令，极大降低顶点计算量。
3. 着色器特效 (AGSL)：曼陀罗的光晕效果可迁移至 Fragment Shader 处理器，利用 GPU 实现实时的内发光与外溢效果。

---

六、 结语

极坐标对称投影是数学秩序对视觉感官的极致献礼。它将转瞬即逝的音频波动锚定在永恒循环的曼陀罗图案中，实现了听觉与视觉在纯粹几何层面的深度耦合。在 Flutter 与鸿蒙系统的协同创新下，这种跨平台的艺术探索正不断证明：代码不仅是功能的载体，更是创造美的画笔。

下篇预告：我们将探索“吸引子（Strange Attractors）”系统，揭秘动力学混沌中的确定性之美。

---

欢迎加入开源鸿蒙跨平台社区： https://openharmonycrossplatform.csdn.net