Flutter跨平台开发实战: 鸿蒙与离散数学系列:计算复杂度与性能红线
本文探讨了OpenHarmony跨平台开发中的性能优化问题,重点介绍了离散数学中的计算复杂度理论及其应用。文章分析了Big O符号在量化算法性能中的作用,阐述了鸿蒙低功耗模式下的复杂度约束标准,并提供了系统架构设计方案和Flutter代码实现。通过对比线性搜索和二分搜索的复杂度差异,展示了如何在高性能列表渲染中应用这些理论。最后总结了离散数学在鸿蒙开发中的核心价值,强调其作为构建高效应用的底层逻辑
代码的优劣不仅在于其逻辑的正确,更在于其在时间和空间尺度上的克制。
前言
在 OpenHarmony 跨平台开发的终极实战中,我们经常面临性能瓶颈:为什么列表滚动会掉帧?为什么在大规模数据检索时应用会卡死?在鸿蒙系统的低功耗模式下,硬件频率受限,对算法效率的要求更是达到了近乎严苛的地步。
离散数学中的**计算复杂度(Computational Complexity)**理论,通过 Big O 符号为我们提供了一把量化性能的标尺。理解增长量级,能让我们在编写代码之初就预见到其在万级、十万级数据下的表现。本篇作为本专栏的收官之作,将带你建立性能评估的数学模型,划定应用的“性能红线”。
目录
- Big O 符号:量化增长的数学语言
- 鸿蒙低功耗模式下的复杂度约束
- 系统架构设计 (UML & 流程)
- Flutter 核心代码实现:复杂度对比分析
- 实战案例演练:高性能列表渲染评估
- 专栏总结:离散数学的逻辑之魂
一、 Big O 符号:量化增长的数学语言
在离散数学中,我们使用大 O 符号描述函数渐近行为的上限。
1. 形式化定义
设 f ( n ) f(n) f(n) 和 g ( n ) g(n) g(n) 是定义在正整数集上的函数。若存在常数 C > 0 C > 0 C>0 和 n 0 n_0 n0,使得对所有 n > n 0 n > n_0 n>n0,都有:![[ |f(n)| \le C|g(n)| ]](https://i-blog.csdnimg.cn/direct/9a4b2ab268db4e0da9ed26a010b54d19.png)
则记作 f ( n ) = O ( g ( n ) ) f(n) = O(g(n)) f(n)=O(g(n))。
2. 常见复杂度等级
| 复杂度 | 增长量级 | 描述 | Flutter 典型场景 |
|---|---|---|---|
| O ( 1 ) O(1) O(1) | 常数级 | 效率极高,不随数据量变化 | Map 查找、ListView.builder 单行渲染 |
| O ( log n ) O(\log n) O(logn) | 对数级 | 效率很高 | 平衡二叉树搜索、二分查找 |
| O ( n ) O(n) O(n) | 线性级 | 随数据量等比例增长 | 简单 List 遍历、非优化列表的全量构建 |
| O ( n 2 ) O(n^2) O(n2) | 平方级 | 效率低下,数据量大时不可用 | 嵌套循环、冒泡排序 |
二、 鸿蒙低功耗模式下的复杂度约束
鸿蒙系统为了延长续航,在低功耗模式下会降低 CPU 核心频率。此时:
- O ( n 2 ) O(n^2) O(n2) 算法会迅速触发系统的“应用无响应 (ANR)”监控。
- 内存复杂度 O ( n ) O(n) O(n) 若过高,会触发系统的垃圾回收(GC)频率增加,进一步导致 UI 抖动。
性能红线:在 UI 主线程中,单次逻辑运算的复杂度应尽可能压低至 O ( n ) O(n) O(n) 以下,而对于列表渲染,必须追求帧内 O ( 1 ) O(1) O(1) 的构建效率。
三、 系统架构设计
我们要构建一个性能分析器,对比不同复杂度算法在处理大规模数据时的真实耗时。
1. 业务流程图 (Flowchart)
2. 系统类图 (UML)
四、 Flutter 核心代码实现:复杂度对比分析
模拟 O ( n ) O(n) O(n) 与 O ( log n ) O(\log n) O(logn) 的性能差异。
核心代码片段:
// 1. 线性搜索:O(n)
int linearSearch(List<int> data, int target) {
for (int i = 0; i < data.length; i++) {
if (data[i] == target) return i;
}
return -1;
}
// 2. 二分搜索:O(log n) - 仅限有序数组
int binarySearch(List<int> data, int target) {
int low = 0, high = data.length - 1;
while (low <= high) {
int mid = (low + high) ~/ 2;
if (data[mid] == target) return mid;
if (data[mid] < target) low = mid + 1;
else high = mid - 1;
}
return -1;
}
五、 实战案例演练
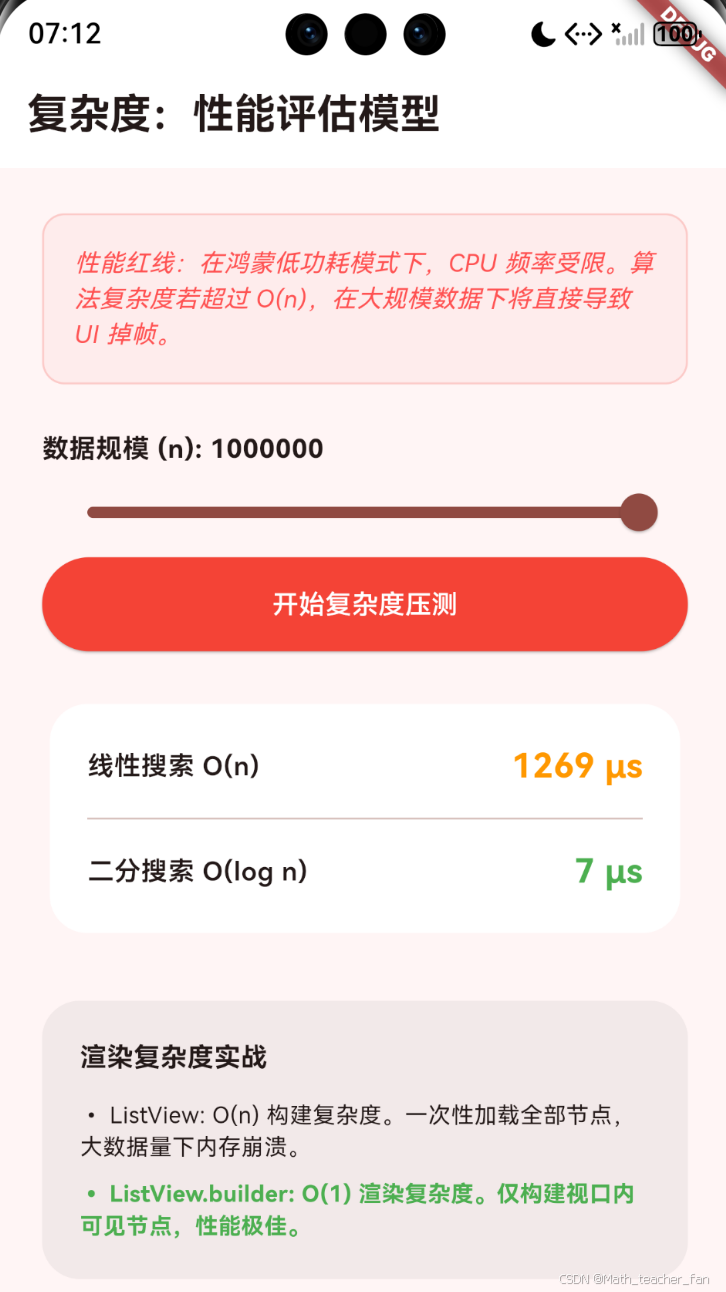
在 lib/main.dart 中,我们实现了一个名为 “Harmony Performance Lab” 的系统:
- 大规模数据模拟:生成从 1,000 到 1,000,000 规模的随机数组。
- 实时压测:对比 O(n) 与 O(log n) 算法在当前硬件下的毫秒级耗时。
- 渲染评估:演示
ListView(全量构建) 与ListView.builder(按需构建) 的复杂度差异,直观展示为何后者是鸿蒙高性能列表的唯一选择。
六、 专栏总结:离散数学的逻辑之魂
至此,《Flutter跨平台开发实战: 鸿蒙与离散数学系列》十篇全部结稿。
我们从集合论的边界出发,历经命题逻辑的严密、图论的交织、树论的层级、状态机的确定、递归的分形、排列组合的多样、二元关系的秩序、数论的唯一,最终抵达了复杂度的红线。
离散数学不是枯燥的公式,而是构建高品质鸿蒙跨平台应用的底层代码基因。 愿每一位开发者都能在代码中融入逻辑之美,在鸿蒙生态中书写性能之巅。
欢迎加入开源鸿蒙跨平台社区:https://openharmonycrossplatform.csdn.net
更多推荐
 已为社区贡献19条内容
已为社区贡献19条内容






所有评论(0)