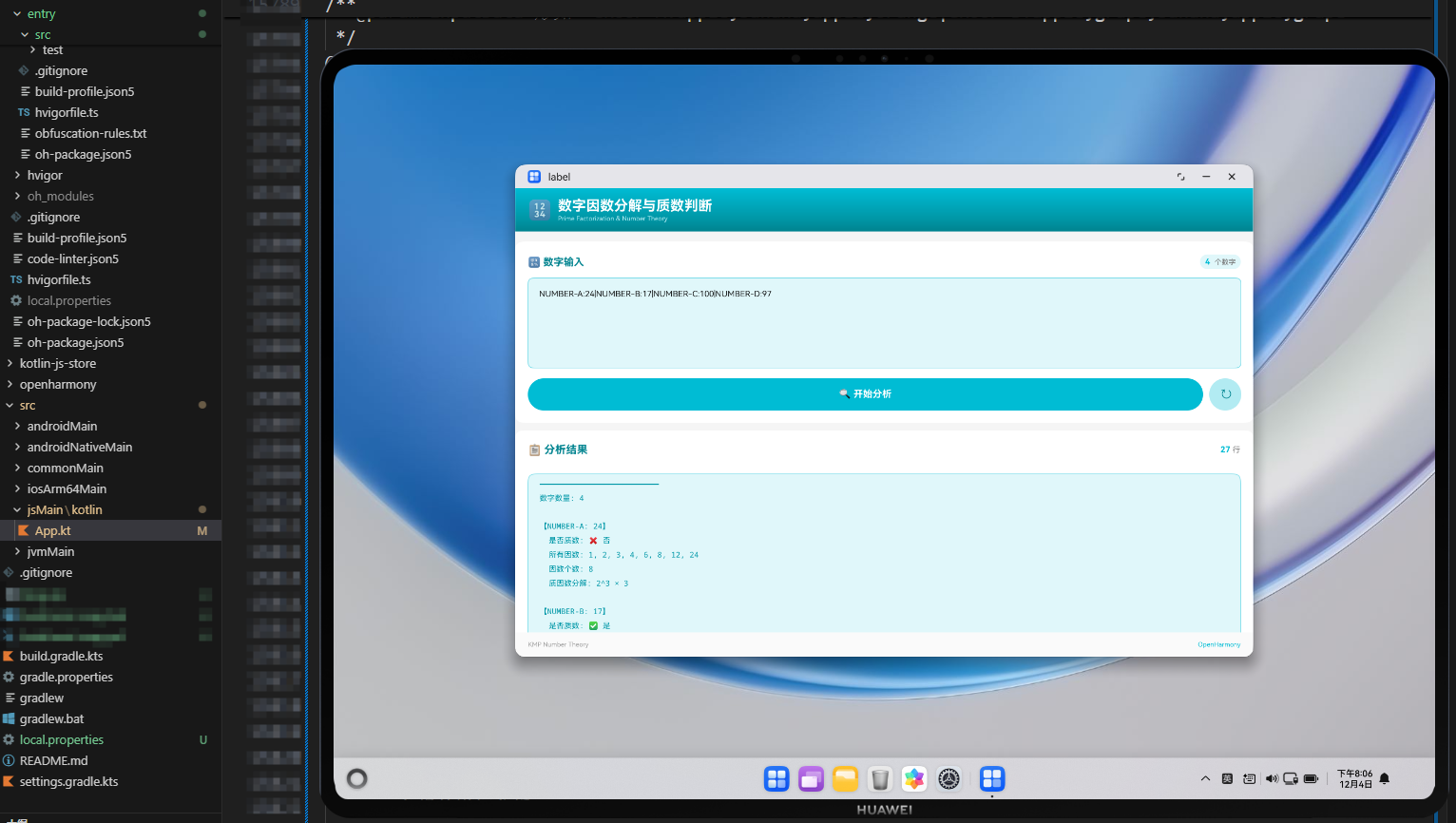
数论算法是计算机科学的基础领域之一。基于 Kotlin Multiplatform（kmp）与 openharmony，我们实现了一个数字因数分解与质数判断工具：输入数字，即可判断是否为质数、获取所有因数、进行质因数分解等，并通过 ArkTS 面板进行可视化呈现。本文包含 Kotlin 数论算法实现、JavaScript 桥接与 ArkTS UI 代码。

Kotlin 数论算法引擎

质数判断算法

private fun isPrimeNumber(n: Long): Boolean {
    if (n < 2) return false
    if (n == 2L) return true
    if (n % 2 == 0L) return false  // 偶数（除了2）都不是质数
    
    var i = 3L
    while (i * i <= n) {  // 只需检查到 sqrt(n)
        if (n % i == 0L) return false
        i += 2  // 只检查奇数
    }
    return true
}

算法优化:

• 排除小于 2 的数
• 2 是唯一的偶数质数，单独处理
• 其他偶数直接返回 false
• 只需检查到 √n，因为如果 n 有大于 √n 的因数，必有对应的小于 √n 的因数
• 只检查奇数（i += 2），进一步优化

时间复杂度: O(√n)

因数分解算法

private fun factorize(n: Long): List<Long> {
    if (n == 1L) return listOf(1L)
    
    val factors = mutableListOf<Long>()
    var num = n
    var i = 1L
    
    while (i * i <= num) {
        if (num % i == 0L) {
            factors.add(i)
            if (i != num / i) {  // 避免重复（如 4 = 2 × 2）
                factors.add(num / i)
            }
        }
        i++
    }
    
    return factors.sorted()
}

算法说明:

• 从 1 开始遍历到 √n
• 如果 i 是因数，则 n/i 也是因数
• 避免平方数重复添加（如 n=4 时，i=2，2 和 4/2=2 是同一个数）

时间复杂度: O(√n)

质因数分解算法

private fun getPrimeFactors(n: Long): Map<Long, Int> {
    val factors = mutableMapOf<Long, Int>()
    var num = n
    var divisor = 2L
    
    while (divisor * divisor <= num) {
        while (num % divisor == 0L) {
            factors[divisor] = factors.getOrDefault(divisor, 0) + 1
            num /= divisor
        }
        divisor++
    }
    
    if (num > 1) {
        factors[num] = factors.getOrDefault(num, 0) + 1
    }
    
    return factors
}

算法说明:

• 使用试除法（Trial Division）
• 从最小的质数 2 开始
• 反复除以当前质数，直到不能整除
• 记录每个质因数的指数
• 最后剩余的 num 如果大于 1，也是质因数

时间复杂度: O(√n)

完整实现代码

@JsExport
fun primeFactorizationAnalyzer(inputData: String): String {
    val sanitized = inputData.trim()
    if (sanitized.isEmpty()) {
        return "❌ 输入为空，请按 NUMBER-A:24|NUMBER-B:17|NUMBER-C:100 格式提供数据"
    }
    
    val numbers = parseNumberSeries(sanitized)
    if (numbers.isEmpty()) {
        return "❌ 未解析到任何数字，请检查格式"
    }
    
    val builder = StringBuilder()
    builder.appendLine("🔢 数字因数分解与质数判断报告")
    builder.appendLine("数字数量: ${numbers.size}")
    builder.appendLine("")
    
    numbers.forEach { (name, num) ->
        val isPrime = isPrimeNumber(num)
        val factors = factorize(num)
        val primeFactors = getPrimeFactors(num)
        
        builder.appendLine("【$name: $num】")
        builder.appendLine("  是否质数: ${if (isPrime) "✅ 是" else "❌ 否"}")
        builder.appendLine("  所有因数: ${factors.joinToString(", ")}")
        builder.appendLine("  因数个数: ${factors.size}")
        if (!isPrime && primeFactors.isNotEmpty()) {
            builder.appendLine("  质因数分解: ${formatPrimeFactorization(primeFactors)}")
        }
        builder.appendLine("")
    }
    
    val primeCount = numbers.count { (_, num) -> isPrimeNumber(num) }
    builder.appendLine("统计: 共 ${numbers.size} 个数字，其中 $primeCount 个是质数")
    
    return builder.toString().trim()
}

JavaScript 桥接函数

import { primeFactorizationAnalyzer } from './hellokjs.js';

export function runPrimeFactorization(payload) {
  const normalized = typeof payload === 'string' ? payload.trim() : '';
  if (!normalized) {
    return '⚠️ 输入为空，请提供 NUMBER-A:24 形式的数据';
  }
  try {
    const report = primeFactorizationAnalyzer(normalized);
    console.info('[prime-factor] success', report.split('\n')[0]);
    return report;
  } catch (error) {
    console.error('[prime-factor] failed', error);
    return `❌ 执行失败: ${error?.message ?? error}`;
  }
}

ArkTS UI 实现

import { primeFactorizationAnalyzer } from './hellokjs';

@Component
struct PrimeFactorizationPanel {
  @State inputData: string = 'NUMBER-A:24|NUMBER-B:17|NUMBER-C:100|NUMBER-D:97';
  @State result: string = '';
  @State loading: boolean = false;

  execute() {
    this.loading = true;
    setTimeout(() => {
      this.result = primeFactorizationAnalyzer(this.inputData);
      this.loading = false;
    }, 100);
  }
}

算法应用场景

1. 密码学

质数在 RSA 加密算法等密码学应用中至关重要，大质数的生成和判断是加密系统的基础。

2. 哈希表优化

哈希表的容量通常选择质数，可以减少哈希冲突，提升性能。

3. 数论研究

因数分解是数论中的基础问题，对于理解数字的性质和规律具有重要意义。

4. 算法竞赛

质数判断和因数分解是算法竞赛中的常见题目，掌握这些算法有助于解决相关问题。

性能优化建议

1. 大数处理

对于非常大的数字（超过 Long 范围），可以考虑：

• 使用 BigInteger
• 实现更高效的算法（如 Pollard’s rho 算法）

2. 质数表缓存

如果需要频繁判断质数，可以预先生成质数表并缓存。

3. Miller-Rabin 算法

对于大质数判断，Miller-Rabin 概率算法可以提供更快的性能（O(k log³ n)），其中 k 是测试次数。

KMP 与 OpenHarmony 集成

通过 Kotlin Multiplatform，数论算法的核心逻辑可以在多个平台共享，而 OpenHarmony 的 ArkTS UI 提供了原生级的用户体验。这种架构设计既保证了代码复用，又确保了良好的性能表现。

总结

本文展示了如何在 KMP 和 OpenHarmony 平台上实现数论算法。通过合理的算法优化（如只检查到 √n、跳过偶数等），我们可以实现高效的质数判断和因数分解。这些算法不仅是计算机科学的基础，在实际应用中也有着广泛的用途。***

v