KMP算法和BF算法都是属于模式串匹配算法

这篇文章将对两种算法做出解释

---

BF算法(暴力求解)

BF算法整体来说就是：按照起始位置的不同，枚举文本串中所有子串，分别与模式串匹配，直到找到一个子串与模式串匹配或者枚举完所有文本串的位置。

BF算法的代码如下：

int BF(char* s, char* p) {
    int sLen = strlen(s);   // 主串长度
    int pLen = strlen(p);   // 模式串长度
    
    //从主串的每个可能的起始位置开始匹配
    for (int i = 0; i <= sLen - pLen; i++) {
        int j;
        // 检查当前位置开始的子串是否与模式串匹配
        for (j = 0; j < pLen; j++) {
            if (s[i + j] != p[j]) {
                break;  // 遇到不匹配的字符，跳出内层循环
            }
        }
        // 如果内层循环完整执行，说明找到了匹配
        if (j == pLen) {
            return i;   // 返回匹配的起始位置
        }
    }
    return -1;  // 没有找到匹配
}

---

KMP算法之大致原理

实际上，KMP算法就是借助预处理数组快速找到文本串中最可能匹配成功的起始位置，而不是都试一遍，从而提升匹配速度。下面，我们使用一个例子来说明KMP算法是如何做的。

如下图，text串中以start为起始位置的子串和mode串进行匹配，由于text[i]!=mode[j]，因而匹配失败：

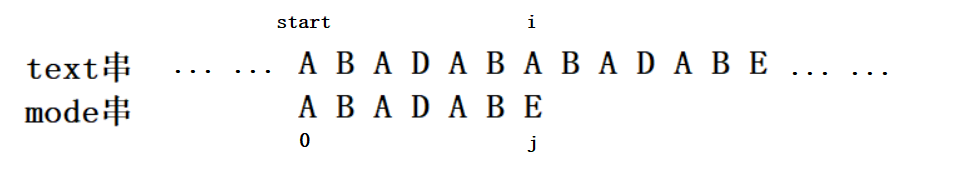
按照暴力算法，下面应该枚举text串中以start+k(k>=1)为起始位置的子串和mode串进行匹配。不过我们可以从这一次的匹配失败中提取出一些信息。

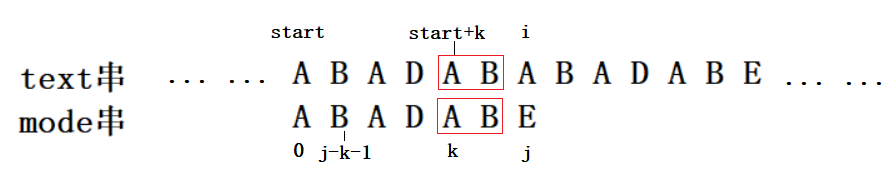
这一次匹配失败，说明mode串的长度肯定大于 i，如果以start+k(i-1>=k>=1)为起始位置的文本子串如果和mode串是匹配的，那么text[start+k,i-1]和mode[0,j-k-1]一定是匹配的，如下所示:

也就是说，只有找到text[start+k,i-1] == mode[0,j-k-1]，以start+k(i-1>=k>=1)为起始位置的文本子串才有可能和mode串是匹配的，才有必要去检查。

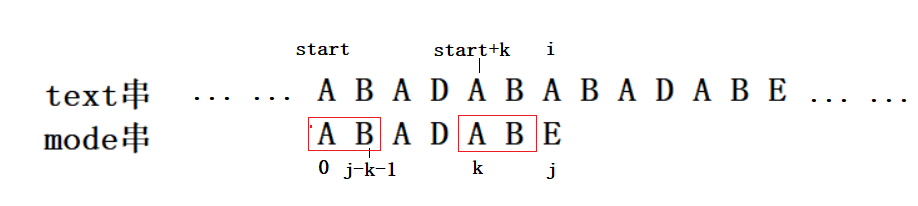
除此之外，从这一次匹配失败的过程中，可以发现text[start~i-1]和mode[0~j-1]是完全相同的，这意味着我们一定可以找到mode[k,j-1] == text[satrt+k~i-1]，如下图所示：

综上所述，假如以start+k(i-1>=k>=1)为起始位置的文本子串和mode串可能匹配，那么一定有mode[0,j-k-1] == mode[k,j-1]。可以看出这两个mode子串长度相同，一个固定起始位置是0，一个固定结束位置是j-1，这两个mode子串是mode串的相同前后缀，如下图所示：

我们不仅知道了下一次应该从start+k(i-1>=k>=1)位置开始匹配mode串，而且也不用回退i指针，因为前面的保证匹配，只需要回退j指针到j-k位置（j-k也就是相同前后缀的长度），然后继续比较字符即可。

还需要考虑一个问题：有多个以start+k(i-1>=k>=1)为起始位置的文本子串和mode串可能匹配。为了不漏掉每一种情况，我们每次寻找的应该是mode串中j位置之前的最长相同前后缀的长度。

还要注意，我们虽然找的是mode串中j位置之前的最长相同前后缀的长度，但它的长度不能超过j，否则下一次检查的还相当于是start为起始位置的文本子串和mode串是否匹配，读者可以画图验证。

我们理顺一下整个编程思路：

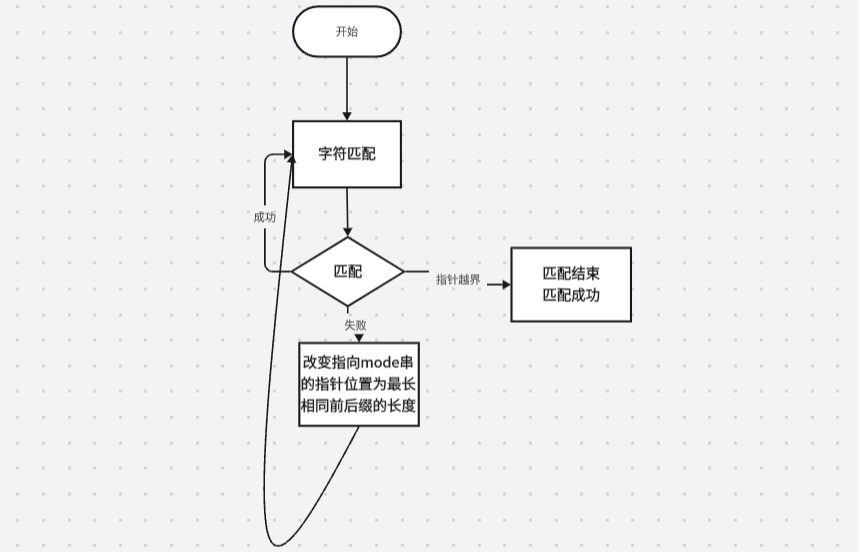
问题的关键在于如何高效的找到mode串中j位置之前的最长相等前后缀的长度，KMP算法构建并使用预处理数组——next。next里面包含的就是mode串中 j（0=<j<mode.size()）位置之前最长相等前后缀的长度。（因此next数组和文本串并无关系，只和mode串有关）

读者请注意：next数组的功能就是给出了每次匹配失败后j回退的位置，从感性的角度理解一下，实际上我们就是使用next数组在已经遍历过的文本串中快速找到最可能匹配成功的起始位置，排除一些注定会失败的检查，从而提升匹配速度。结果就是指向文本串的i指针不会回退。

---

KMP算法之next数组

next[i]表示的是i位置之前mode串的最长相等前后缀的长度，前缀或后缀的长度小于i（当这个长度等于i时，和原来匹配失败的字符串一样，不需要检查）。因此可以联想到next[i+1]的值只可能和next[0]~next[i]以及mode[0]~mode[i]有关系，所以我们把注意力放到next[i+1]的前边来：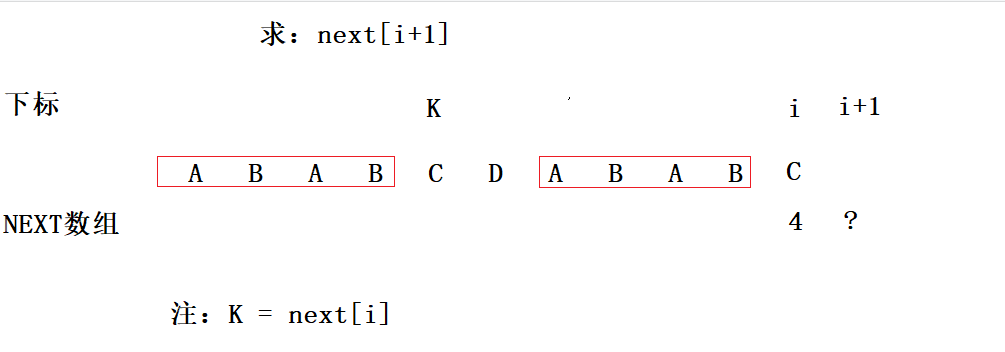

我们可以发现，mode[k] == mode[i]，也就是说，next[i+1]至少是next[i]（k）+1,如下图蓝色线框：

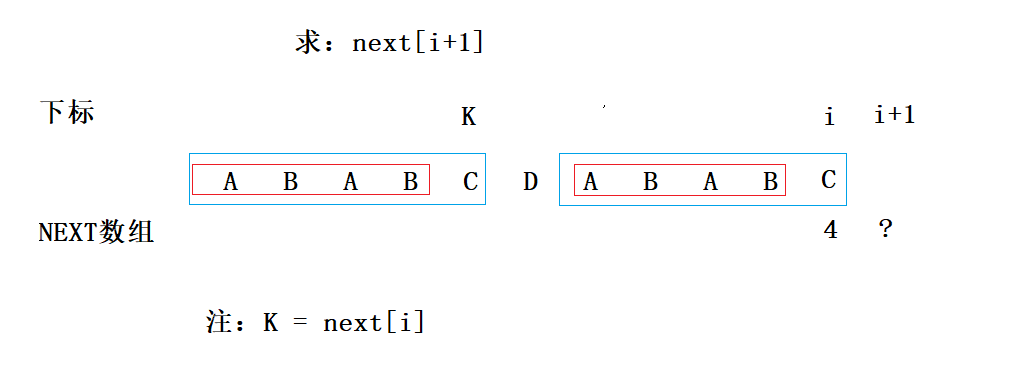
那么next[i+1]是否还能更大呢？好，我们假设它还能更大，如下图紫色框：

现在请读者明白，我们假设：紫色线框内的两个字符串是相等的（尽管看上去不相等）。并且此时，红色线框的字符串也相等，我们把两个紫色线框的内容放到一起对比一下：

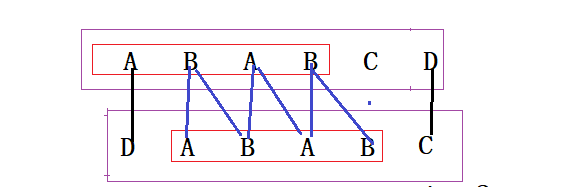
不难看出，由第一条蓝色线段相连的两个元素相等（由于紫色线框内的字符串相等）和第二个蓝色线段相连的元素相等（由于红色线框内的字符串相等），可以推出红色线框内的第一个元素和第二个元素相等。同理，根据第三条和第四条蓝色线段可以推出红色线框内的第二个元素和第三个元素相等，根据第四条和第五条蓝色线段可以推出红色线框内的第三个元素和第四个元素相等。至此，我们推断出，红色线框的所有元素两两相等。又因为第一条，第二条黑色线段相连的两个元素相等（由于紫色线框内的字符串相等），于是，我们推断出了紫色线框内的所有元素也是两两相等。

如果按以上推论，mode串应该是这样的：

那么，next[i]应该等于9而不是4。假设和已存在的事实相冲突，假设不成立。

当然，爱刨根问底的读者可能并不认可这个结论，因为假如两个红色线框之间的元素个数有更多，即，紫色线框没有重合部分或者刚好连起来了，这个结论可能不成立，所以读者可以按照上述方法再验证各种情况，结论是一样的。

好了，回到我们刚才所说的，next[i+1]不可能更大，即得出结论:if(mode[k] == mode[i])next[i+1] = next[i]（k）+1;

那么如果说mode[k] ！= mode[i]呢（也就是i位置的值不是‘C’）？我们接下来讨论的就是这种情况，如下图：

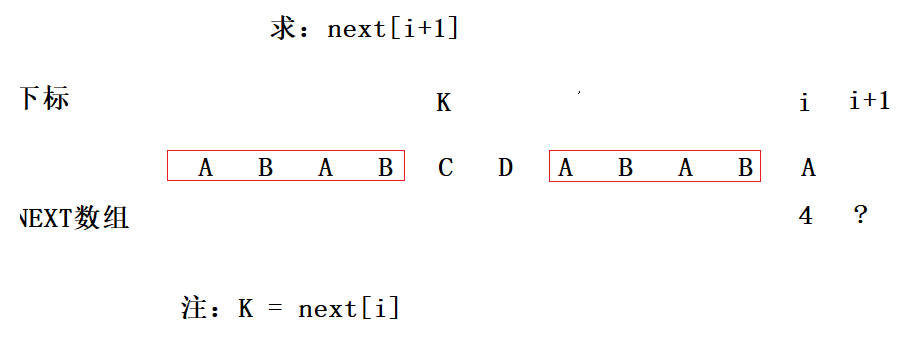
在这种情况下，next[i+1]的值肯定小于next[i]（k）+1,也就是小于5。那么next[i+1]剩下的可能值就是4,3,2,1,0。我们只需要依次判断next[i+1]是不是4,3,2,1,0，一旦发现是，就不用继续往下判断了，因为要求的是最长的相等前后缀。

那么问题来了，该如何判断next[i]是否等于4呢？假设next[i+1] = 4，如下图：

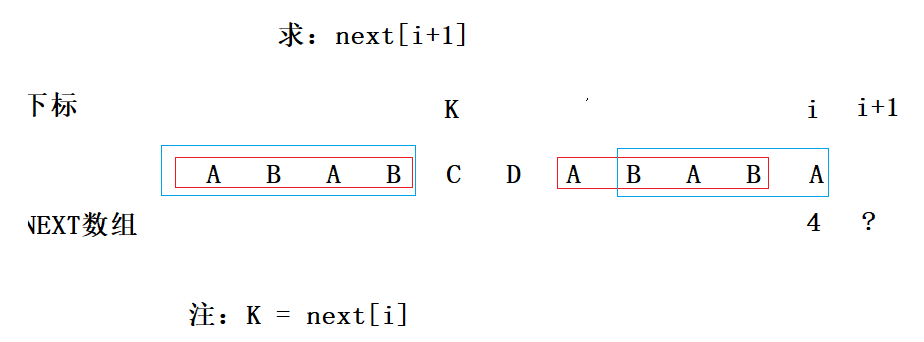
只需要判断两个蓝色线框内的字符串是否相等即可知道next[i+1]是否可以等于4，那我们再进一步，如下图：

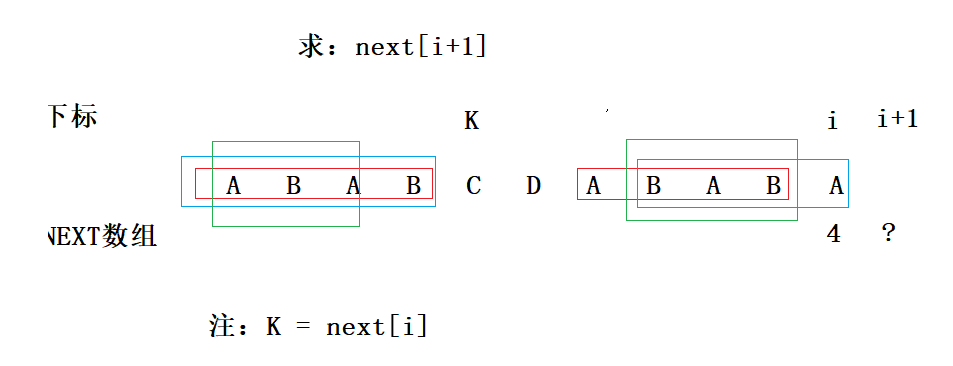
只需要判断两个绿色线框字符串是否相等以及mode[i]是否等于mode[k-1]，就知道next[i+1]是否可以等于4。观察可以发现，两个绿色框的内容是红色框内字符串的一对前后缀（由于两个红色框的字符串是相等的），如下图：

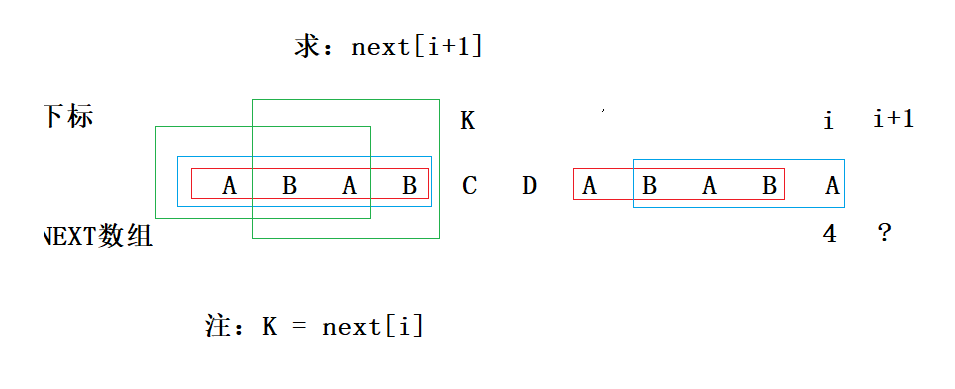
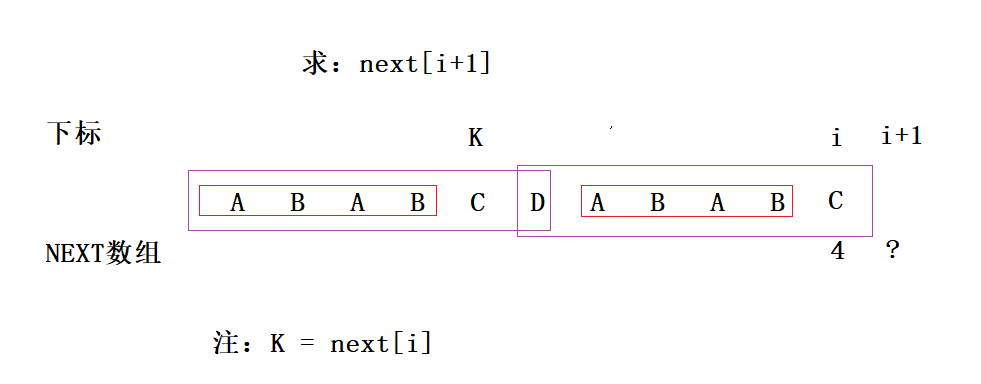
所以next[i+1] = 4 <=> mode[0~k-1]中有长度为k-1的相同前后缀 && mode[i] == mode[k-1]。

同理，可得出next[i+1] = 3/2/1的等价条件（next[i+1] = 0 相当于没有匹配的，可以留作默认填充）。

最终可得：

1. next[i+1] = 4(k) <=> mode[0~k-1]中有长度为k-1的相同前后缀 && mode[i] == mode[k-1]
2. next[i+1] = 3(k-1)<=> mode[0~k-1]中有长度为k-2的相同前后缀 && mode[i] == mode[k-2]
3. next[i+1] = 2(k-2)<=> mode[0~k-1]中有长度为k-3的相同前后缀 && mode[i] == mode[k-3]
4. next[i+1] = 1(k-3)<=> mode[0~k-1]中有长度为k-4的相同前后缀 && mode[i] == mode[k-4]
5. next[i+1] = 0(k-4)<=> mode[0~k-1]中有长度为k-5的相同前后缀 && mode[i] == mode[k-5]

注：可以发现next[i+1] = 相同前后缀的长度+1

但是我们只知道next[k],也就是最长的相等前后缀是多少，从这一点出发。

假如next[k] == k-2（第二条情况）,那么可以确定的是，mode[0~k-1]中一定没有长度为k-1的相同前后缀，因为既然next[k] == k-2，说明最长相同前后缀最大也就是k-2。因此第二条前面的所有情况的第一个条件肯定都不满足，没必要看了。

而后面的几种情况是否要看取决于mode[i] 是否等于 mode[k-2]（mode[k-2] == mode[next[k]]，因为此时next[k] == k-2）：

如果mode[i] == mode[k-2]（mode[next[k]]）,那两个条件都满足了（mode[0~k-1]中有长度为k-2的相同前后缀 && mode[i] == mode[k-2]），说明next[i+1]可以等于3（即next[k]+1）,此时没有必要再列举下面的几种情况了，因为他们的值都比3小。

在上图所举的例子中，就是这种情况：                                                                                    mode[i] == mode[k-2]（mode[next[k]]）,所以next[i+1] = next[k]+1 = 3。

如果mode[i] != mode[k-2]（mode[next[k]]），说明我们得考虑第二种之后的一些情况。为了方便讲解这种情况，我把mode字符串中i位置的字符修改成不是A的字符，如下图：                    读者要记住，此时的条件如下（可以多看几遍，容易忘了前面的条件）：

1. next[k] == k-2（也就是2），但是mode[i]!=mode[k-2]（mode[next[k]]）。
2. 两个红框内的字符串相等，两个绿框内的字符串相同

此时的目标是依次判断下面情况看是否成立：

1. next[i+1] = 2(k-2)<=> mode[0~k-1]中有长度为k-3的相同前后缀 && mode[i] == mode[k-3]
2. next[i+1] = 1(k-3)<=> mode[0~k-1]中有长度为k-4的相同前后缀 && mode[i] == mode[k-4]
3. next[i+1] = 0(k-4)<=> mode[0~k-1]中有长度为k-5的相同前后缀 && mode[i] == mode[k-5]

由于剩下的需要判断的情况中，要找的相同前后缀的长度都小于k-2（也就是2，绿框的长度），并且两个绿框内的字符串都相同，实际上可以把问题转换成找第一个绿框内的对字符串的相同前后缀：

1. next[i+1] = 2(next[k])<=> mode[0~next[k]-1]中有长度为next[k]-1的相同前后缀 && mode[i] == mode[next[k]-1]
2. next[i+1] = 1(next[k]-1)<=> mode[0~next[k]-1]中有长度为next[k]-2的相同前后缀 && mode[i] == mode[next[k]-2]
3. next[i+1] = 0(next[k]-2)<=> mode[0~next[k]-1]中有长度为next[k]-3的相同前后缀 && mode[i] == mode[next[k]-3]

读者有没有发现？接下来的问题就变成了和我们最开始的问题:判断一些情况是否成立，只是把k替换成了next[k]（情况多少取决于区间大小，这不影响他们的题目类型一样）：在解决问题的过程中遇到类似的问题，递归诞生了：

• 每次都先判断mode[i]和mode[next[k]]（k = next[i]）是否相等，如果相等，就说明next[i+1] = next[k]+1；否则，就让k = next[k],然后再继续上述判断，循环往复。

那么递归的出口在哪儿？我们可以发现如果mode[i]一直不等于mode[next[k]]，那么k就会一直更新。并且我们发现next[x]一定是小于x且大于等于0（至少x>0的时候是这样的，next[0]我们没有填写）。

因此如果进入递归的时候k>0,那么k在更新过程中一直在缩小且是非负数，当k第一次更新到0的时候（k一定会更新到0），说明之前判断过：mode[i]！=mode[0]，因此没必要继续回退了，next[i+1]只能是0了。这就是递归的出口，我们需要对它进行处理。

至于刚进入递归时是 k== 0 的情况，我们可以另外考虑，写完代码再合并到递归逻辑里面，这样子写代码比较清晰

理顺一下求next数组的思路：

初始化next数组：next[1] = 0;

k = next[i];//i>=1，因此k>=0,不会越界
if(mode[i] == mode[k])//如果相等，next[i+1]最大就是k+1;
{
    next[i+1] = k+1;  
}
else//如果不相等就要依次判断各种情况。
{
    while(k!=0 && mode[i] != mode[next[k]])//为true表示这种情况不成立，需要继续判断剩余情况                                                                         
    {
        k = next[k];//某种情况不成立，考虑它后面的剩余的情况，
    }
    if(k == 0)next[i+1] = 0;
    else
    next[i+1] = next[k] + 1; //如果最后一个元素相等，即两个条件都满足了，即证明这种情况是成立的
}

从这个代码中我们可以发现，next[0]始终是没有被访问的，因为k == 0的时候被特殊处理。所以单纯对于填充next数组来说，next[0]想初始化为什么都是可以的，但如果是要用next数组来匹配，next[0]的值会有一些别的用处，下面会说。

以上只是求一个next[x]的值的代码，接下来是填充整个next数组的代码：

vector<int> Getnext(const string& mode)
{
    int n = mode.size();
    vector<int> next(n);
    next[0] = -1;
    next[1] = 0;

    for(int i = 2;i<next.size();i++) 
    {
        int k = next[i - 1];
        if (mode[k] == mode[i - 1])next[i] = k + 1;
        else 
        {
            while(k!=0 && mode[i-1]!=mode[next[k]])
            {
                k = next[k];
            }
            if (k == 0)next[i] = 0;
            else next[i] = next[k] + 1;
        }
    }
    return next;
}

---

KMP算法实现

vector<int> Getnext(const string& mode)
{
    int n = mode.size();
    vector<int> next(n);
    next[0] = -1;
    next[1] = 0;

    for(int i = 2;i<next.size();i++) 
    {
        int k = next[i - 1];
        if (mode[k] == mode[i - 1])next[i] = k + 1;
        else 
        {
            while(k!=0 && mode[i-1]!=mode[next[k]])
            {
                k = next[k];
            }
            if (k == 0)next[i] = 0;
            else next[i] = next[k] + 1;
        }
    }
    return next;
}

int Kmp(string text,string mode) 
{
    int lentext = text.size();
    int lenmode = mode.size();

    if (lentext < lenmode)return -1;

    vector<int> next = Getnext(mode);//获取填充完毕的next数组

    int i = 0, j = 0;

    while(i<lentext && j<lenmode)
    {
        if (j==-1 || text[i] == mode[j])
        {
            i++;
            j++;
        }
        else 
        {
            j = next[j];//如果j是0，j被更新为-1。此时 j=0 && text[i] != mode[j],那么下一步应该j++(j=0);i++;
        }
    }
    if (j >= lenmode)//如果说是因为mode串匹配结束而跳出循环，就说明找到了,返回起始位置下标。
        return i - lenmode;
    else //如果说是因为text串匹配结束而跳出循环，就说明没找到。
        return -1;
}

在KMP主函数的匹配过程中，如果text[i]!=mode[j]，j就会回退，i不动。而当j == 0&& text[i]!=mode[j]的时候，j = next[0],使用到了next[0]的值。

所以next[0]的值应该设置为多少呢，这要看我们此时的情况：j == 0&& text[i]!=mode[j]，这说明mode[0]和mode[i]都不匹配，因此此时要做的是：i++,j = 0。

所以我们把next[0]设置为-1，再给if添加一个条件，就可以优雅的让i++,j = 0；

当然，也可以不这样做，那么我们就要在j = next[j]语句之前判断一下j是否等于0，并进行特殊处理：

if(j == 0)
{
    i++;
    j=0;
}
else j = next[j];

---

KMP算法的时间复杂度

对于KMP主函数：

• 每次j回退，都是在已经遍历过的文本串中快速找到了一个可能匹配成功的起始位置。所以j的回退总次数最大也就是lentext(总共也就这么多可选的起始位置)。
• 又因为i不会回退，所以移动的次数也是lentext。

KMP主函数中的while循环执行的总次数就是if执行的次数(i移动)+else执行的次数(j回退)，也就是2*lentext，所以KMP主函数的时间复杂度为O(lentext)。

对于Getnext函数也就是求next数组的过程：

被数学证明是O(lenmode)时间复杂度

所以总的时间复杂度为O(lenmode+lentext)。