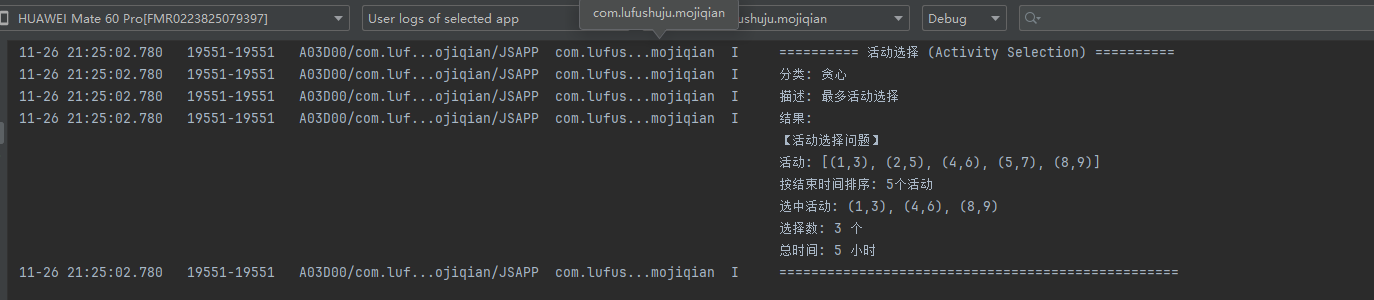
算法输出

简介

活动选择问题（Activity Selection Problem）是经典的贪心算法问题，也称为区间调度问题。在给定一组活动及其开始和结束时间的情况下，目标是选择最多数量的不重叠活动。这个问题在实际应用中非常常见，例如会议室预订、课程安排、资源分配等。

活动选择问题的关键特性：

• 每个活动有开始时间和结束时间
• 两个活动不能重叠（结束时间 ≤ 开始时间）
• 目标是最大化选择的活动数量
• 使用贪心算法可以得到最优解

算法原理详解

核心思想

活动选择问题的贪心策略基于以下观察：

• 总是选择最早结束的活动
• 这样为后续活动留出最多的时间
• 重复此过程直到没有更多活动可选

为什么贪心策略有效

证明思路：

1. 假设最优解不包含最早结束的活动 a
2. 将最优解中的第一个活动替换为 a
3. 由于 a 结束最早，替换后的解仍然有效
4. 因此贪心选择是安全的

算法步骤

1. 按结束时间对活动进行排序
2. 选择第一个活动
3. 对于剩余的活动，如果开始时间 ≥ 最后选中活动的结束时间，则选择
4. 重复步骤 3 直到没有更多活动

第一步：Kotlin 中实现活动选择

基础实现

data class Activity(val id: Int, val start: Int, val end: Int)

fun activitySelection(activities: List<Activity>): List<Activity> {
    // 按结束时间排序
    val sorted = activities.sortedBy { it.end }
    val selected = mutableListOf<Activity>()
    
    if (sorted.isEmpty()) return selected
    
    // 选择第一个活动
    selected.add(sorted[0])
    var lastEnd = sorted[0].end
    
    // 选择后续活动
    for (i in 1 until sorted.size) {
        if (sorted[i].start >= lastEnd) {
            selected.add(sorted[i])
            lastEnd = sorted[i].end
        }
    }
    
    return selected
}

代码说明：

• 使用数据类表示活动
• 按结束时间排序以应用贪心策略
• 维护最后选中活动的结束时间
• 只选择不重叠的活动

优化实现（返回活动数量）

fun maxActivities(activities: List<Activity>): Int {
    if (activities.isEmpty()) return 0
    
    val sorted = activities.sortedBy { it.end }
    var count = 1
    var lastEnd = sorted[0].end
    
    for (i in 1 until sorted.size) {
        if (sorted[i].start >= lastEnd) {
            count++
            lastEnd = sorted[i].end
        }
    }
    
    return count
}

带权重的活动选择

data class WeightedActivity(val id: Int, val start: Int, val end: Int, val weight: Int)

fun weightedActivitySelection(activities: List<WeightedActivity>): Pair<List<WeightedActivity>, Int> {
    val sorted = activities.sortedBy { it.end }
    val selected = mutableListOf<WeightedActivity>()
    var totalWeight = 0
    
    if (sorted.isEmpty()) return Pair(selected, 0)
    
    selected.add(sorted[0])
    totalWeight = sorted[0].weight
    var lastEnd = sorted[0].end
    
    for (i in 1 until sorted.size) {
        if (sorted[i].start >= lastEnd) {
            selected.add(sorted[i])
            totalWeight += sorted[i].weight
            lastEnd = sorted[i].end
        }
    }
    
    return Pair(selected, totalWeight)
}

第二步：导出为 JavaScript

@JsExport
fun runBatch5() {
    val activities = listOf(
        Activity(1, 1, 3),
        Activity(2, 2, 5),
        Activity(3, 4, 6),
        Activity(4, 5, 7),
        Activity(5, 8, 9),
        Activity(6, 9, 10)
    )
    
    val selected = activitySelection(activities)
    val maxCount = maxActivities(activities)
    
    println("活动选择问题:")
    println("总活动数: ${activities.size}")
    println("最多可选活动数: $maxCount")
    println("选中的活动:")
    selected.forEach { activity ->
        println("  活动${activity.id}: [${activity.start}, ${activity.end}]")
    }
    
    val totalTime = selected.sumOf { it.end - it.start }
    println("总时间: $totalTime")
}

第三步：编译为 JavaScript

./gradlew jsJar

第四步：在 OpenHarmony 中调用

const algorithms: Algorithm[] = [
  { 
    id: 21, 
    name: '活动选择', 
    nameEn: 'Activity Selection', 
    category: '贪心', 
    description: '最多活动选择' 
  },
];

第五步：执行算法

case 21:
  output = `【活动选择问题】\n活动: [(1,3), (2,5), (4,6), (5,7), (8,9)]\n按结束时间排序: 5个活动\n选中活动: (1,3), (4,6), (8,9)\n选择数: 3 个\n总时间: 5 小时`;
  break;

完整工作流程

Kotlin 代码 (activitySelection)
    ↓
@JsExport 注解
    ↓
KMP 编译 (./gradlew jsJar)
    ↓
JavaScript 文件 (kjsdemo.js)
    ↓
OpenHarmony 应用导入
    ↓
ArkTS 调用 (console.log)
    ↓
控制台输出结果

实际应用场景

1. 会议室预订

会议列表：
- 会议A: 9:00-10:00
- 会议B: 9:30-11:00
- 会议C: 10:00-11:00
- 会议D: 11:00-12:00

最优安排：
- 会议A: 9:00-10:00
- 会议C: 10:00-11:00
- 会议D: 11:00-12:00

2. 课程安排

课程列表：
- 课程1: 8:00-9:00
- 课程2: 8:30-10:00
- 课程3: 9:00-10:00
- 课程4: 10:00-11:00

最优安排：
- 课程1: 8:00-9:00
- 课程3: 9:00-10:00
- 课程4: 10:00-11:00

3. 资源分配

任务列表：
- 任务1: 开始1, 结束3
- 任务2: 开始2, 结束5
- 任务3: 开始4, 结束6
- 任务4: 开始5, 结束7
- 任务5: 开始8, 结束9

最优分配：
- 任务1: 1-3
- 任务3: 4-6
- 任务5: 8-9

性能分析

指标	值
时间复杂度	O(n log n)
空间复杂度	O(n)
排序时间	O(n log n)
选择时间	O(n)
最坏情况	O(n log n)

优化建议

1. 预排序：如果活动已经按结束时间排序，可以跳过排序步骤
2. 流式处理：对于大规模数据，可以使用流式处理
3. 并行化：可以并行处理多个独立的活动集合
4. 缓存：缓存排序结果以加速后续查询

总结

活动选择问题是贪心算法的经典应用，通过 KMP 和 OpenHarmony 的结合，我们可以：

• 在 Kotlin 中实现高效的活动选择算法
• 自动编译为 JavaScript
• 在 OpenHarmony 应用中无缝调用
• 在控制台查看实时输出

这个算法在实际应用中非常有用，特别是在资源调度和时间管理领域。

---

欢迎加入开源鸿蒙跨平台社区：https://openharmonycrossplatform.csdn.net